This post is a summary and paper skimming on regularization and optimization. So, this post will be keep updating by the time.
Paper List
Regularization
- Regularizing neural networks by penalizing confident output distributions, ICLR2017, Google, Geoffrey Hinton
Optimization
- Gradient acceleration in activation functions
- Paper
- Sangchul Hahn, Heeyoul Choi (Handong Global University)
- Cyclical learning rates for training neural networks
- Paper
- Leslie N. Smith (U.S. Naval Research Laboratory)
- Super-Convergence: very fast training of neural networks using large learning rates
- Paper
- Leslie N. Smith (U.S. Naval Research Laboratory), Nicholay Topin (university of Maryland)
Regularizing neural networks by penalizing confident output distributions
- Conference: ICLR2017
Summary
- Research Objective
- To suggest the wide applicable regularizers
- Proposed Solution
- Regularizing neural networks by penalizing low entropy output distributions
- Penalizing low entropy output distributions acts as a strong regularizer in supervised learning.
- Connect a maximum entropy based confidence penalty to label smoothing through the direction of the KL divergence.
- When the prior label distribution is uniform, label smoothing is equivalent to adding the KL divergence between the uniform distribution \(u\) and the network’s predicted distribution \(p_\theta\) to the negative log-likelihood.
- By reversing the direction of the KL divergence in equation (1), \(D_{KL}(u \parallel p_\theta(y \mid x))\), it recovers the confidence penalty.
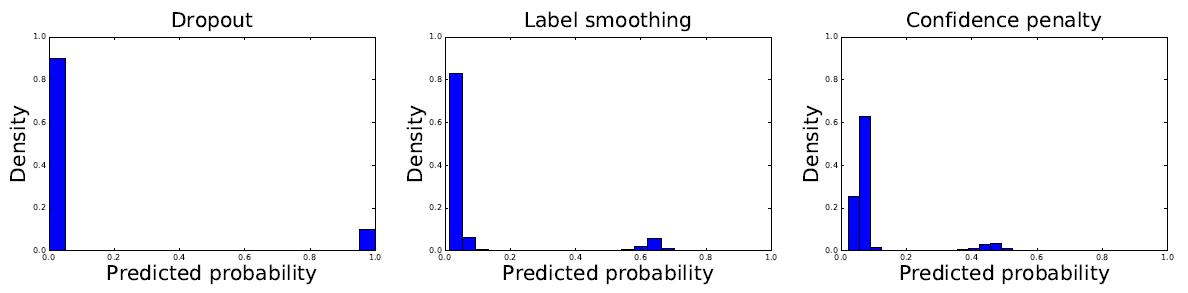 Figure: Distribution of the magnitude of softmax probabilities on the MNIST validation set. A fully-connected, 2-layer, 1024-unit neural network was trained with dropout (left), label smoothing (center), and the confidence penalty (right). Dropout leads to a softmax distribution where probabilities are either 0 or 1. By contrast, both label smoothing and the confidence penalty lead to smoother output distributions, which results in better generalization.
Figure: Distribution of the magnitude of softmax probabilities on the MNIST validation set. A fully-connected, 2-layer, 1024-unit neural network was trained with dropout (left), label smoothing (center), and the confidence penalty (right). Dropout leads to a softmax distribution where probabilities are either 0 or 1. By contrast, both label smoothing and the confidence penalty lead to smoother output distributions, which results in better generalization.
- Contribution
- Both label smoothing and the confidence penalty improve state-of-the-art models across benchmarks without modifying existing hyperparameters
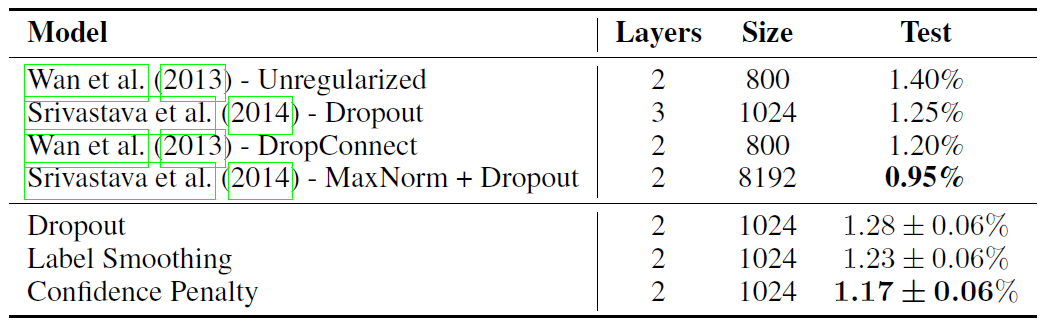 Figure: Test error (%) for permutation-invariant MNIST.
Figure: Test error (%) for permutation-invariant MNIST.