Regularization and Optimization

This post is a summary and paper skimming on regularization and optimization. So, this post will be keep updating by the time.

Paper List

Regularization

• Regularizing neural networks by penalizing confident output distributions, ICLR2017, Google, Geoffrey Hinton
  • Paper

Optimization

• Gradient acceleration in activation functions
  • Paper
  • Sangchul Hahn, Heeyoul Choi (Handong Global University)
• Cyclical learning rates for training neural networks
  • Paper
  • Leslie N. Smith (U.S. Naval Research Laboratory)
• Super-Convergence: very fast training of neural networks using large learning rates
  • Paper
  • Leslie N. Smith (U.S. Naval Research Laboratory), Nicholay Topin (university of Maryland)

Regularizing neural networks by penalizing confident output distributions

• Conference: ICLR2017

Summary

• Research Objective
  • To suggest the wide applicable regularizers
• Proposed Solution
  • Regularizing neural networks by penalizing low entropy output distributions
  • Penalizing low entropy output distributions acts as a strong regularizer in supervised learning.
  • Connect a maximum entropy based confidence penalty to label smoothing through the direction of the KL divergence.
    • When the prior label distribution is uniform, label smoothing is equivalent to adding the KL divergence between the uniform distribution \(u\) and the network’s predicted distribution \(p_\theta\) to the negative log-likelihood.
    • By reversing the direction of the KL divergence in equation (1), \(D_{KL}(u \parallel p_\theta(y \mid x))\), it recovers the confidence penalty.

\[\mathcal{L}(\theta)=-\sum \log p_\theta (y\mid x)-D_{KL}(u \parallel p_\theta(y \mid x)) \cdots (1)\]

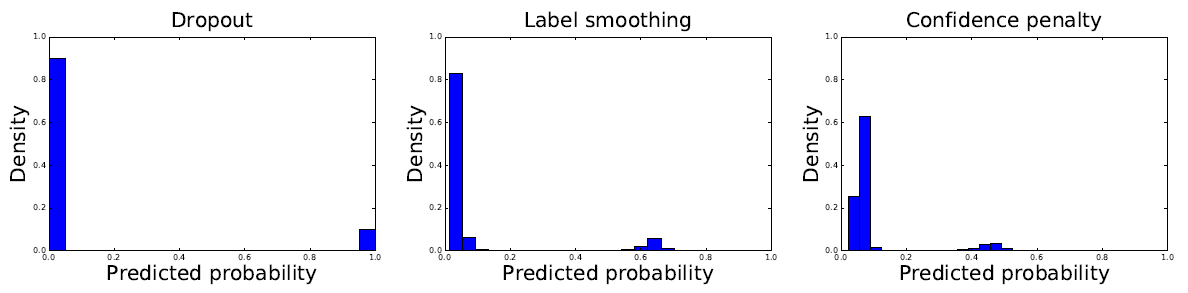Figure: Distribution of the magnitude of softmax probabilities on the MNIST validation set. A fully-connected, 2-layer, 1024-unit neural network was trained with dropout (left), label smoothing (center), and the confidence penalty (right). Dropout leads to a softmax distribution where probabilities are either 0 or 1. By contrast, both label smoothing and the confidence penalty lead to smoother output distributions, which results in better generalization.

• Contribution
  • Both label smoothing and the confidence penalty improve state-of-the-art models across benchmarks without modifying existing hyperparameters

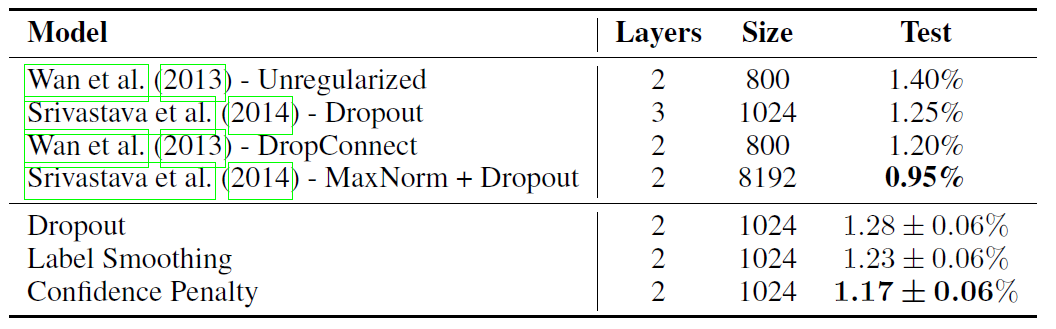Figure: Test error (%) for permutation-invariant MNIST.

References

• Paper: Regularizing neural networks by penalizing confident output distributions