“Improved deep metric learning with multi-class N-pair loss objective” proposes a way to handle the slow convergence problem of contrastive loss and triplet loss. This paper was presented in the Advances in Neural Information Processing Systems (NIPS) 2016 by Kihyuk Sohn from NEC laboratories america.

Summary

  • Problem Statement
    • Existing frameworks of deep metric learning based on contrastive loss and triplet loss often suffer from slow convergence.
    • Partially because they employ only one negative example while not interacting with the other negative lcasses in each update.
  • Research Objective
    • To address the problem of conventional metric learning methods.
  • Proposed Solution: multi-class N-pair loss
    • The proposed objective function generalizes triplet loss by allowing joint comparison among more than one negative examples (\(N-1\) negative examples)
    • And reduces the computational burden of evaluating deep embedding vectors via an efficient batch construction strategy using only \(N\) pairs of examples, instead of \((N+1) \times N\).
  • Contribution
    • Proposed loss is superior to the triplet loss as well as other competing loss functions

Preliminary: Distance Metric Learning

Let \(x \in X\) be an input data and \(y \in \{1, ..., L\}\) be its output label.

  • \(x^+\): positive examples which are from the same class
  • \(x^-\): negative examples which are not from the same class
  • The kernel \(f(\cdot ; \theta): X \rightarrow \mathbb{R}^K\): takes \(x\) and generates an embedding vector \(f(x)\).

Contrastive Loss

Contrastive loss takes pair of examples as input and trains a network to predict whether two inputs are from the same class or not.

\[L_{cont}^m (x_i,x_j;f)=1\{y_i=y_j\}\parallel f_i - f_j \parallel _2^2 + 1\{y_i \neq y_j\}\max(0,m-\parallel f_i - f_j \parallel _2)^2\]
  • \(m\) is a margin parameter imposing the distance between examples from different classes to be larger than \(m\).

Triplet Loss

Triplet loss is composed of triplets, each consisting of a query, a positive example (to the query), and a negative example. Compared to contrastive loss, triplet loss only requires the difference of (dis-)similarities between positive and negative examples to the query point to be larger than a margin \(m\).

\[L_{tri}^m (x,x^+,x^-;f)=\max(0,\parallel f - f^+ \parallel _2^2-\parallel f - f^- \parallel _2^2+m)\]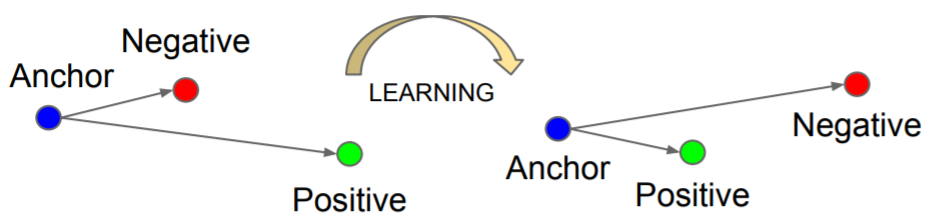

Triplet Loss Figure 1: The triplet loss minimizes the distance between an anchor and a positive, both of which have the same identity, and maximizes the distance between the ancor and a negative of a different identity.

N-pair Loss

N-pair loss is a generalized version of triplet loss having one anchor, one positive sample and (N-1) negative samples. If \(N=2\), it is the same with triplet loss.

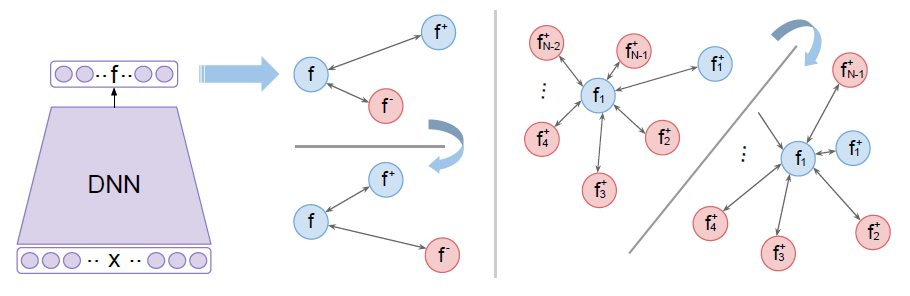N-pair Loss Figure 2: Deep metric learning with triplet loss (left) and (N+1)-tuplet loss (right).

  • Learning to identify from multiple negative examples
    • (N+1)-tuplet loss identifies a positive example from \(N\) negative examples.
    • N-pair loss function:
\[L(\{x,x^+,\{x_i\}_{i=1}^{N-1}\};f) = \log\left( 1 + \sum_{i=1}^{N-1}{\exp(f^{T}f_i - f^Tf^+)}\right)\]

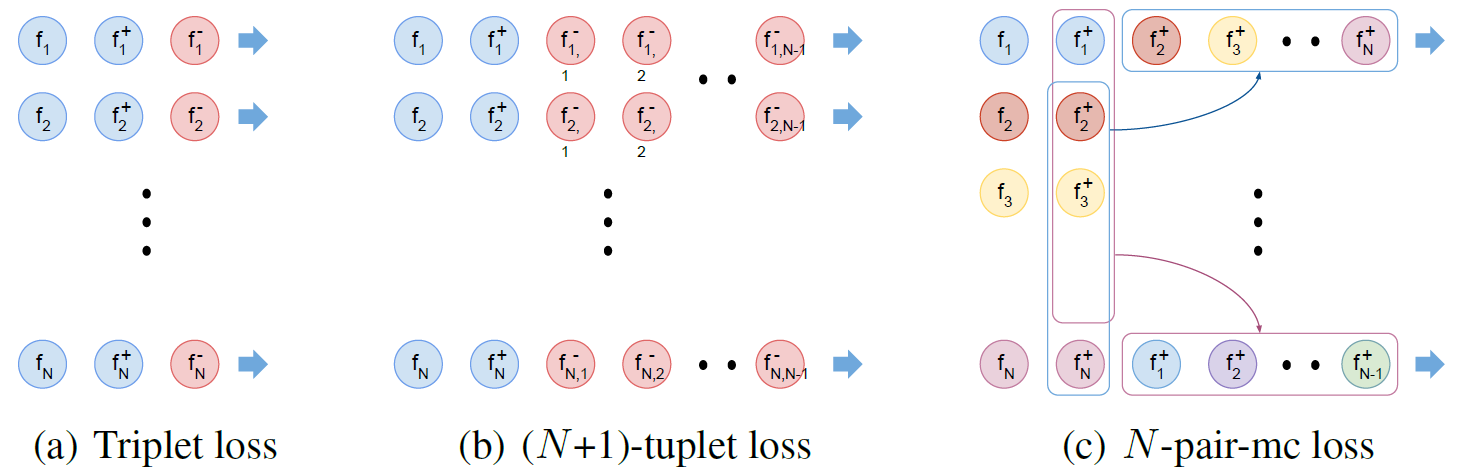Loss comparision Figure 3: Triplet loss, (N+1)-tuplet loss, and multi-class N-pair loss with training batch construction.

  • Efficient batch construction via N-pair examples: \(O(N^2) \rightarrow O(N)\)
    • N tuples of (N+1)-tuplet loss requires \(N(N+!)\) examples to be evaluated.
    • We can obtain N tuples of (N+1)-tuplet loss by constructing a batch with N pairs whose pairs are from different classes. This requires only \(2N\) examples to be evaluated.
    • Multi-class N-pair (N-pair-mc) loss:
\[L_{N-pair-mc}\left(\{(x_i, x_i^+)\}_{i=1}^N;f\right) = \frac{1}{N} \sum_{i=1}^N \log{\left(1+\sum_{j \neq i}{\exp{(f_i^{T}f_j^+ - f_i^T f_i^+)}} \right)}\]
  • Hard negative class mining
    • When output space is small, N-pair loss doesn’t require hard negative data mining.
    • When output space is large, we propose to find hard negative “classes”.

Experimental Results

Fine-grained visual object recognition and verification

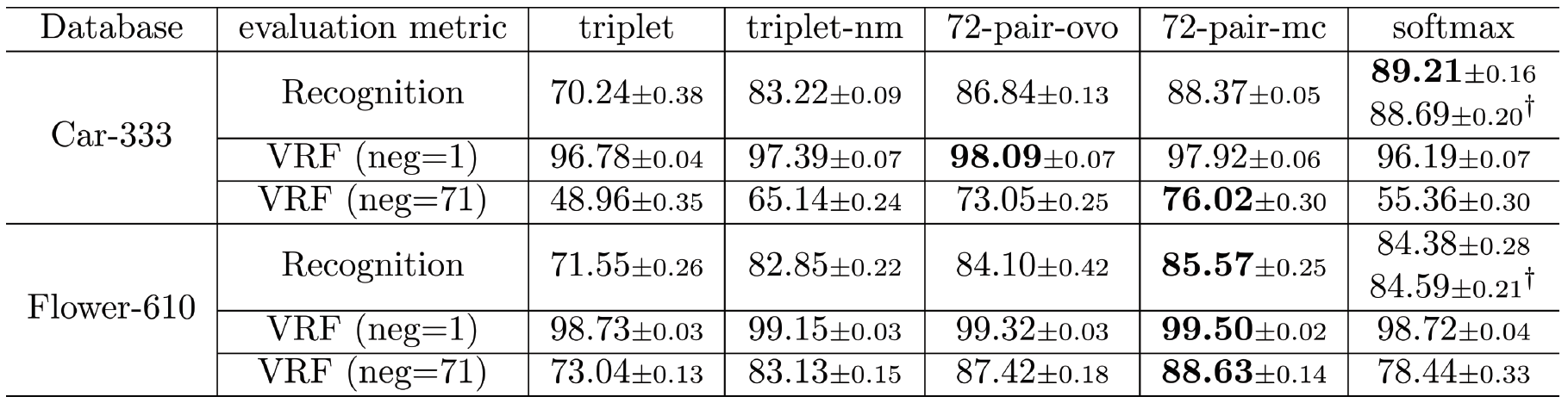ex1 Figure 4: Mean recognition and verification accuracy with standard error on the test set of Car-333 and Flower-610 datasets. The recognition accuracy of all models are evaluated using kNN classifier; for models with softmax classifier, we also evaluate recognition accuracy using softmax classifier (y). The verification accuracy (VRF) is evaluated at different numbers of negative examples.

Visual recognition of unseen object classes

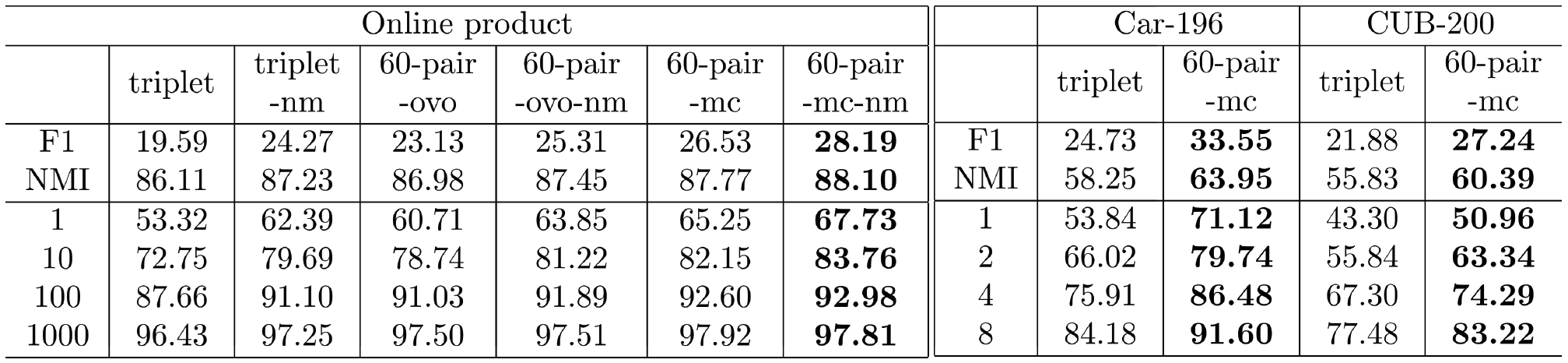ex2 Figure 5: F1, NMI, and recall@K scores on the test set of online product, Car-196, and CUB-200 datasets. F1 and NMI scores are averaged over 10 different random seeds for kmeans clustering but standard errors are omitted due to space limit. The best performing model and those with overlapping standard errors are bold-faced..

Face verification and identification

ex3 Figure 6: Mean verification accuracy (VRF) with standard error, rank-1 accuracy of closed set identification and DIR@FAR=1% rate of open-set identification on LFW dataset. The number of examples per batch is fixed to 384 for all models except for 320-pair-mc model.

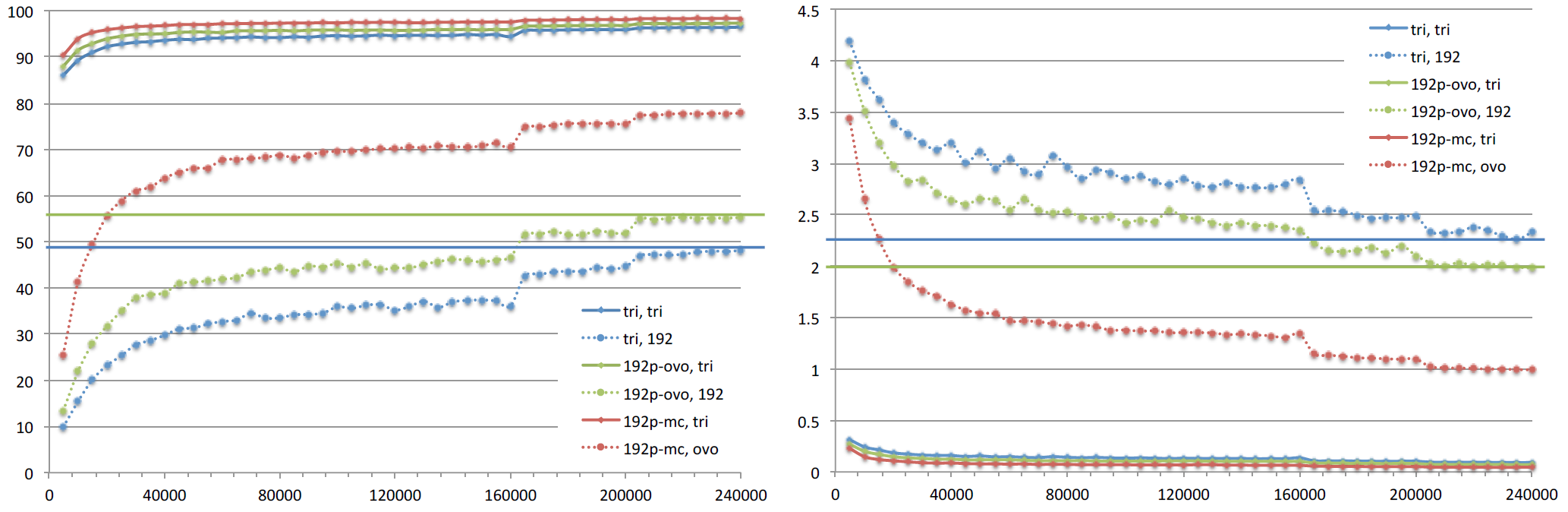ex4 Figure 7: Training curve of triplet, 192-pair-ovo, and 192-pair-mc loss models onWebFace database. We measure both (a) triplet and 192-pair loss as well as (b) classification accuracy.

ex5 Figure 8: Verification and rank-1 accuracy on LFW database. For model name of N x M, we refer N the number of different classes in each batch and M the number of positive examples per class.

References

You May Also Enjoy