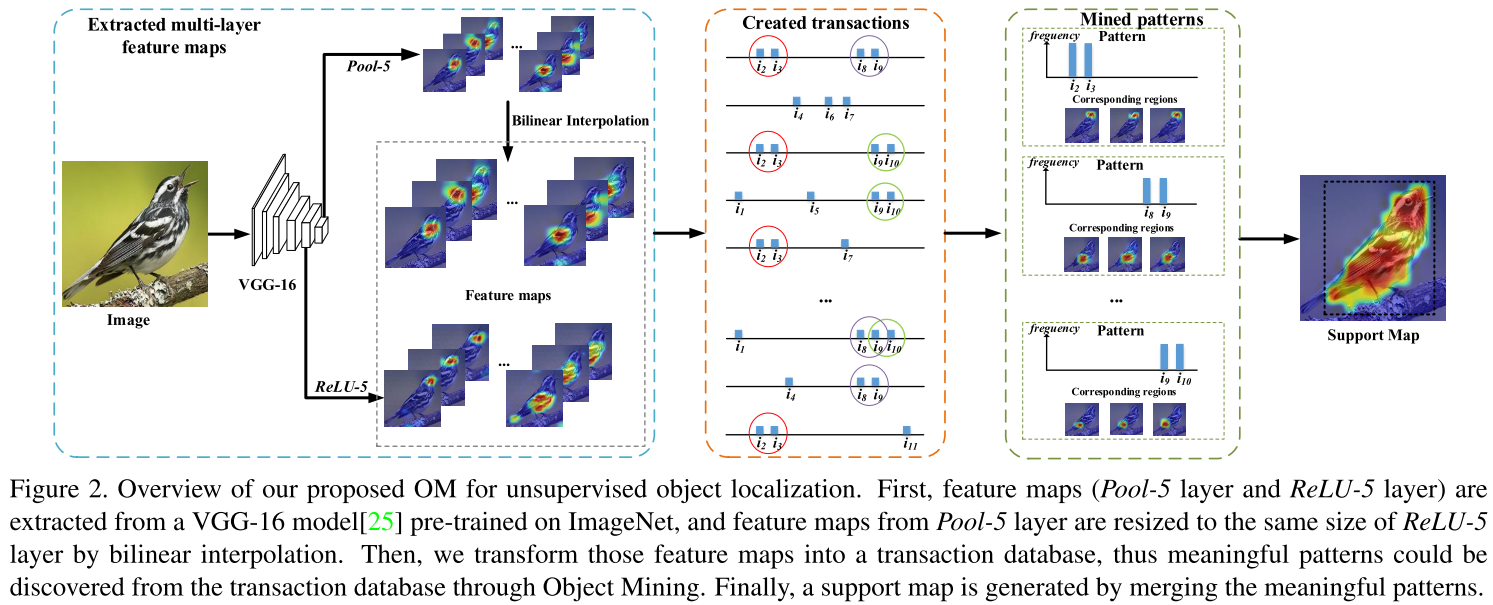
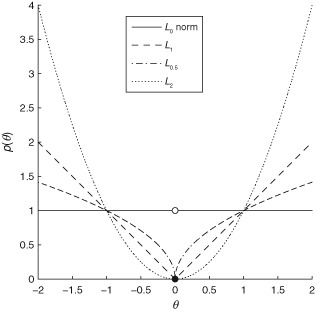
When we train a deep learning model, we need to set a loss function for minimizing the error. The loss function indicates how much each variable contributes to the value to be optimized in the problem.
Loss function
In deep learning context, the Loss function is a function that measures the quality of a particular set of parameters based on how well the output of the network agrees with the ground truth labels in the training data.
- The loss function is used to guide the training process in order to find a set of parameters that reduce the value of the loss function
- loss function = cost function = objective function = error function
- Loss function can be written as an average over loss functions for individual training examples:
Empirical Risk Minimization (ERM)
Let a loss function \(C(y, y')\) be given that penalizes deviations between the true class and the estimated one. The Empirical Risk (the average loss or error of an estimator) of a decision strategy is the total loss:
\[R(e) = \sum_l C(y_l, e(x_l)) \rightarrow min_e\]It should be minimized with respect to the decision strategy \(e\).
For Regression
For regression problem, network predicts continuous, and numeric variables. Loss functions for regression problem includes absolute value, square error, etc.
L1-Norm (Absolute Value)
L1-norm loss function minimizes the sum of the absolute differences \(\mathcal{L}\) between the target value \(y_i\) and the estimated values \(f_{\theta}(x_i)\).
\[\mathcal{L}=\frac{1}{n}\sum_{i=1}^{n}\mid y_i - f_{\theta}(x_i) \mid\]- Pros
- Produces sparser solutions
- Good in high dimensional spaces
- Prediction speed
- Robust: less sensitive to outliers
- Produces sparser solutions
- Cons
- Unstable solution (possibly multiple solutions)
- Computational inefficient on non-sparse cases
L2-Norm (Square Error, Euclidean Loss)
L2-norm loss function minimize the sum of the square of the differences \(\mathcal{L}\) between the target value \(y_i\) and the estimated values \(f_{\theta}(x_i)\).
\[\mathcal{L}=\frac{1}{n}\sum_{i=1}^{n} (y_i - f_{\theta}(x_i))^2\]- Pros
- More precise and better than L1-norm
- Penalizes large errors more strongly
- Stable solution (always one solution)
- Cons
- Sensitive to outliers
- Computational efficient due to having analytical solutions
For Classification
For classification problem, network predicts categorical variables. Loss function for classification problem includes hinges loss, cross-entropy loss, etc.
Square Loss
Square loss is more commonly used in regression, but it can be utilized for classification by re-writing as a function \(\phi(yf(\vec{x}))\).
\[V(f(\vec{x}),y) = (1-yf(\vec{x}))^2\]The square loss function is both convex and smooth and matches the 0–1 when \(yf(\vec{x})= 0\) and when \(yf(\vec{x}) = 1\).
Hinge Loss
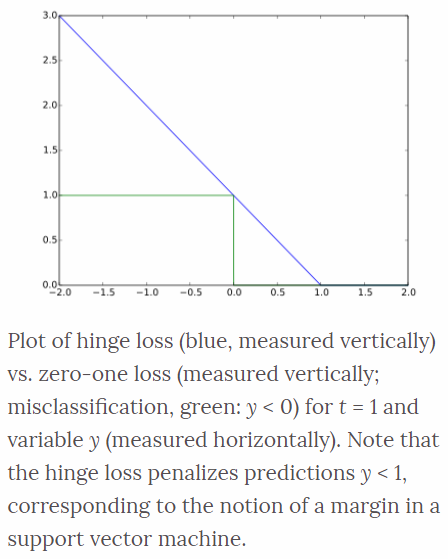
The hinge loss is used for maximum-margin classification task, most notably for support vector machines (SVMs). For an intended output \(t=±1\), a classifier score \(y\) which should be the raw output of the classifier’s decision function, not the predicted class label.
\[\ell(y) = \max(0, 1-t \cdot y)\]For example, in linear SVMs, \(y=wx+b\) where \((w,b)\) are the parameters of the hyperplane and \(x\) is the point to classify. When \(t\) and \(y\) have the same sign (\(y\) predicts the right class) and \(\mid y \mid \geq 1\), the hinge loss \(ell(y) = 0\). When they have opposite sign, \(ell(y)\) increases linearly with \(y\).
Logistic Loss
Logistic loss displays a similar convergence rate to the hinge loss function, and since it is continuous, gradient descent methods can be utilized. The logistic loss function is defined as
\[V(f(\vec{x}),y) = \frac{1}{\ln 2}\ln(1+e^{-yf(\vec{x})})\]Cross Entropy Loss
Cross entropy loss is commonly used loss function for deep neural network training. It is closely related to the Kullback-Leibler divergence between the empirical distribution and the predicted distribution. It is not naturally represented as a product of the true label and the predicted value, but it is convex and can be minimized using stochastic gradient descent methods. Using the alternative label convention \(t=(1+y)/2\) so that \(t \in {0,1}\), the cross entropy loss is defined as,
\[V(f(\vec{x}),t) = -t\ln(f(\vec{x}))-(1-t)\ln(1-f(\vec{x}))\]