Feed-Forward Neural Network (FFNN)

The Feed-Forward Neural Network (FFNN) is the simplest and basic artificial neural network we should know first before talking about other complicated networks.

Feed-Forward Neural Network (FFNN)

A feed-forward neural network is an artificial neural network wherein connections between the units do not form a cycle. - Wikipedia

FFNN is often called multilayer perceptrons (MLPs) and deep feed-forward network when it includes many hidden layers. It consists of an input layer, one or several hidden layers, and an output layer when every layer has multiple neurons (units). Each connection between neurons is associated with weight and bias.

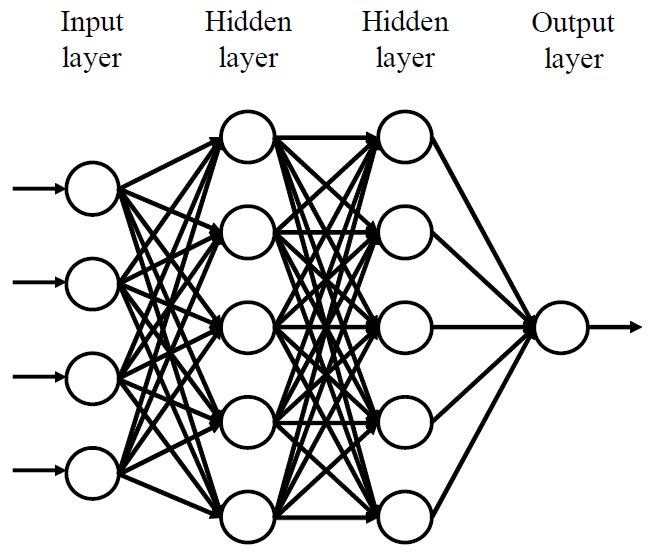
Forward Propagation

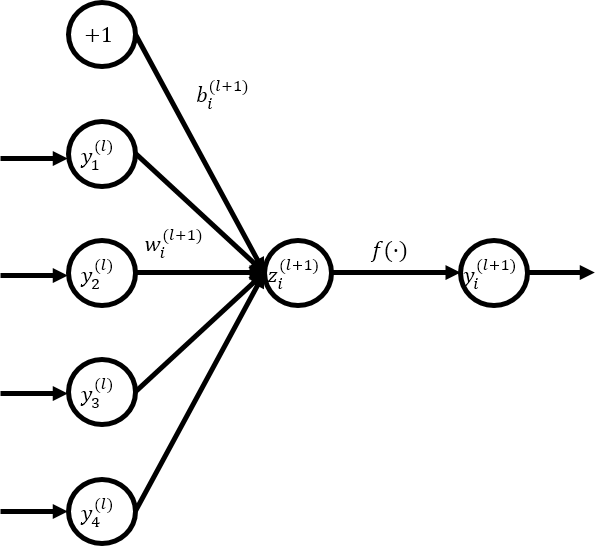
Consider a FFNN with \(L\) hidden layers, \(l\in\{1,...,L\}\) is index of the hidden layers. The forward propagation process of FFNN can be described as below.

\[z^{(l+1)}_{i} = \mathbf{w}^{(l+1)}_{i}\mathbf{y}^{(l)} + b^{(l+1)}_{i}, \\ y^{(l+1)}_{i} = f(z^{(l+1)}_{i}).\]

• \(\mathbf{z}^{(l)}\): the vector of inputs into layer \(l\)
• \(\mathbf{y}^{(l)}\): the vector of outputs from layer \(l\)
  • \(\mathbf{y}^{(1)}\) equals to \(\mathbf{x}\) as the input
• \(i\): any hidden unit
• \(\mathbf{W}^{(l)}\): a weight matrix in the layer \(l\)
• \(\mathbf{b}^{(l)}\): a bias vector in the layer \(l\)
• \(f(\cdot)\): an activation function such as a sigmoid, hyperbolic tangent, rectified linear unit, or softmax function

Backpropagation

In the backpropagation step, the neural network can be trained with gradient descent algorithm. The main goal of this step is to minimize the error function \(J(\mathbf{W},\mathbf{b})\) such as cross entropy for the classification problem and mean-squared error for the regression problem. The gradient descent algorithm updates the parameters \(\mathbf{W}\) and \(\mathbf{b}\) in every iteration as below.

\[\mathbf{W}_{ij}^{(l)} \leftarrow \mathbf{W}_{ij}^{(l)} - \alpha \frac{\partial}{\partial \mathbf{W}_{ij}^{(l)}} J(\mathbf{W},\mathbf{b}), \\ b_{i}^{(l)} \leftarrow b_{i}^{(l)} - \alpha \frac{\partial}{\partial b_{i}^{(l)}} J(\mathbf{W},\mathbf{b}).\]

• \(W^{(l)}_{ij}\): an element of the weight matrix associated with the connection between unit \(j\) in layer \(l\) and unit \(i\) in layer \(l+1\)
• \(b^{(l)}_i\): an element of the bias vector associated with unit \(i\) in layer \(l+1\) and \({\alpha}\) is the learning rate

References

• FFNN in Wikipedia [Link]
• Deep Learning book [Link]