Capsule Network

Cpasule Network is a new types of neural network proposed by Geoffrey Hinton and his team and presented in NIPS 2017. As Geoffrey Hinton is Godfathers of Deep Learning, everyone in this field was crazy about this paper. Moreover, the capsule network is proposed to solve problems of current convolutional neural network and achieves state-of-the-art performance on MNIST data set. We are going to talk about how the capsule network works and what the difference between capsule network and CNN is.

Introduction

Drawback of Convolutional Neural Networks (CNNs)

CNNs have been suffered from a couple of drawbacks,

• CNNs give poor performance if there is rotation, tilt or any other different orientation in image.
• Each layer in CNN understands an image at a much more granular level (slow increase in receptive field).

In order to handle these problem, people attempt to use several techniques,

• Data Augmentation: artificially creates new data from original training data through different ways of processing or combination of multiple processing, such as shifts, flips, rotation, shear and so on.
• Pooling: creates summaries of each sub-region and helps to reduce training time. And it gives the model to have positional and translational invariance in object detection.

However, both attempt still have limitation,

• Using Data Augmentation to deal with every transformation of images is inefficient and impossible to cover all possibilities.
• Positional invariance from Pooling can cause false positive for images which have the same components but not in a correct order. In the example images of ship below, we can easily see both are different, but CNN can consider both are matching.

What we need is not invariance but equivariance,

• Invariance makes a CNN tolerant to small changes in the view point.
• Equivariance makes a CNN understand the rotation or proportion change and adapt itself accordingly so that the spatial positioning inside an image is not lost. In the images of ship below, even though both are ship, CNN will reduce its size to detect smaller ship, but Capsule Networks will handle this problem.

Capsule Network

Capsules

A capsule is a group of neurons whose activity vector represents the instantiation parameters of a specific type of entity such as an object or an object part.

• Activity vector
  • Length: estimated probability that the entity exists
  • Orientation: object’s estimated pose parameters

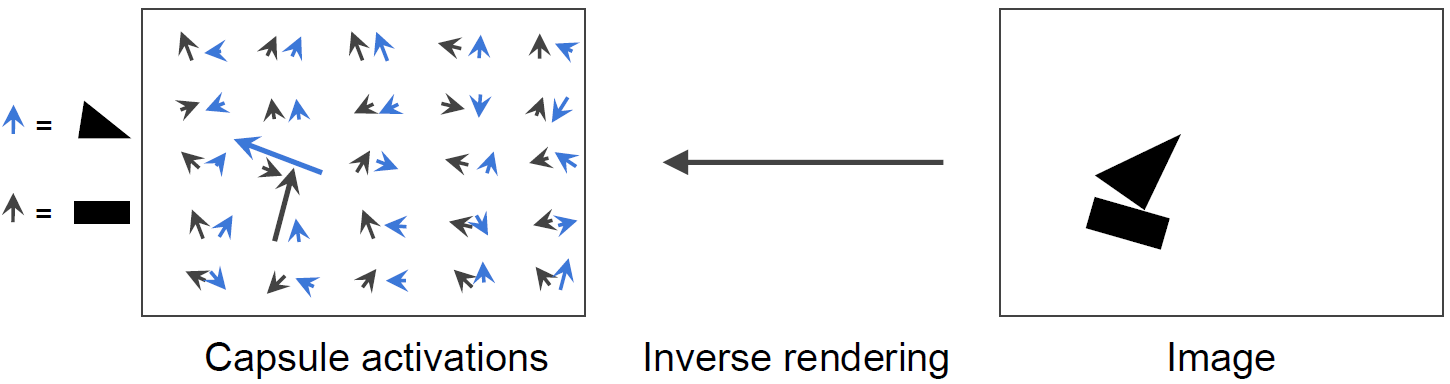
Dynamic Routing Algorithm

Squashing is a non-linear function to ensure that short vectors get shrunk to almost zero length and long vectors get shrunk to a length slightly below 1.

\[v_{j}=\frac{\parallel s_{j} \parallel^{2}}{1+{\parallel s_{j} \parallel}^{2}}\frac{s_{j}}{\parallel s_{j} \parallel}\]

where \(v_{j}\) is the vector output of capsule \(j\) and \(s_{j}\) is its total input.

\[s_{j}=\sum_i c_{ij} \hat{u}_{j\mid i} \\ \hat{u}_{j\mid i} = W_{ij}u_{i} \\ c_{ij}=\frac{\exp{(b_{ij})}}{\sum_k \exp{(b_{ik})}}\]

• \(s_{j}\) is a weighted sum over all prediction vectors \(\hat{u}_{j\mid i}\) from the capsules in the layer below
• \(\hat{u}_{j\mid i}\) is calculated by multiplying the output \(u_{i}\) of a capsule in the layer below by a weight matrix \(W_{ij}\)
• \(c_{ij}\) are coupling coefficients between capsule \(i\) and all the capsules in the layer above which sum to 1 and are determined by a routing softmax
• \(b_{ij}\) are the log prior probabilities that capsule \(i\) should be coupled to capsule \(j\)

The initial coupling coefficients are iteratively refined by measuring the agreement between the current output \(v_{j}\) of each capsule \(j\) in the layer above and the prediction \(\hat{u}_{j\mid i}\) made by capsule \(i\). The agreement is calculated by scalar product of \(a_{ij}=v_{j} \cdot \hat{u}_{j\mid i}\).

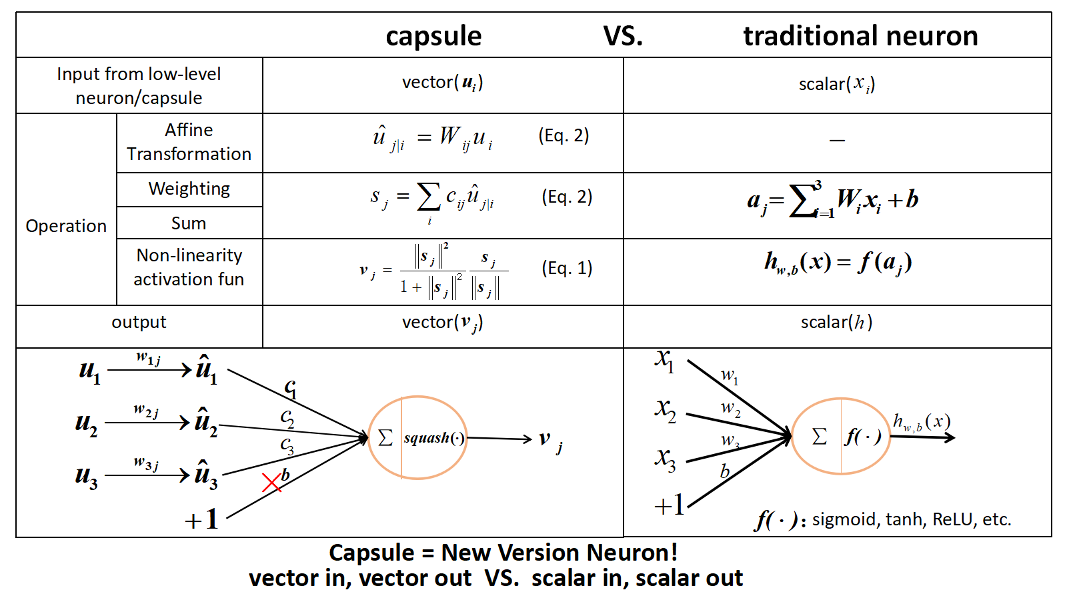
Capsule V.S. Neuron

Margin Loss for Digit Existence

For each digit capsule \(k\), loss function \(L_k\) is a separate margin loss as,

\[L_{k}=T_{k} \max(0, m^{+}-\parallel v_k \parallel)^2+\lambda(1-T_k) max(0, \parallel v_k \parallel - m^-)^2\]

where \(T_k=1\) iff a digit of class \(k\) is present and \(m^+=0.9\) and \(m^-=0.1\). \(\lambda\) is down-weighting of the loss for absent digit classes which is set \(\lambda=0.5\) as default. The total loss is the sum of the losses of all digit capsules.

CapsNet Architecture

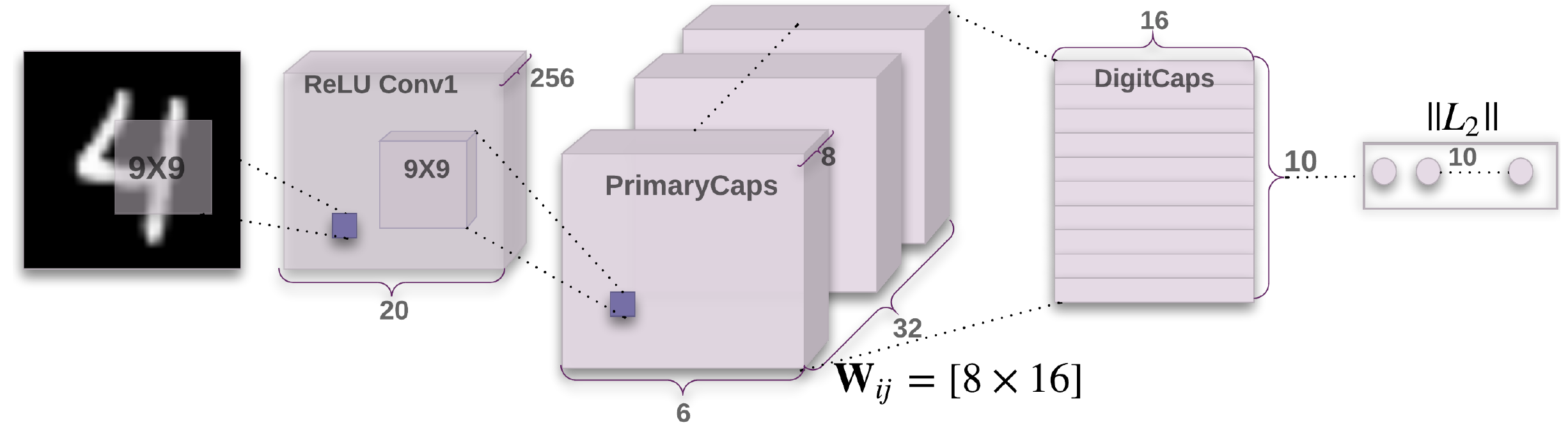
• A simple CapsNet from the figure has only two convolutional layers and one fully connected layer
• Cov1 has 256, \(9 \times 9\) convolutional kernels with a stride of 1 and ReLU activation.
• PrimaryCaps is a convolutional capsule layer with 32 channels of convolutional 8D capsules.
• DigitCaps is a final layer with one 16D capsule per digit class and each of htese capsules receives input from all the capsules in the layer below.
• Routing algorithm is used only between two consecutive capsule layers, because there is no orientation in its space to agree on for Conv1.

Reconstruction as a Regularization Method

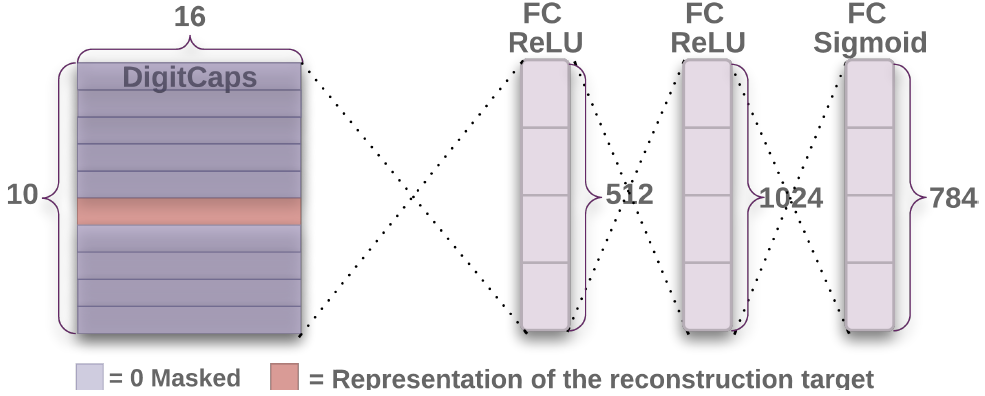
• In order to encourage the digit capsule to encode instantiation parameters of the input digits, we add reconstruction loss to margin loss using a decoder with 3 fully connected layers.

\[\textrm{Loss} = \textrm{margin loss} + \alpha \, \textrm{reconstruction loss}\]

• The reconstruction loss is the squared difference between the reconstructed image and the input image. (\(\alpha=0.0005\) in the paper)

• The figure shows a sample MNIST test reconstructions of a CapsNet with 3 routing iterations.
• \((l,p,r)\) represents the label, the prediction and the reconstruction target respectively.
• The two rightmost columns show failure example and rest of them are correct example.
• It shows robustness of 16D output of the CapsNet while keeping only important details.

Capsules on MNIST

Experiment Result

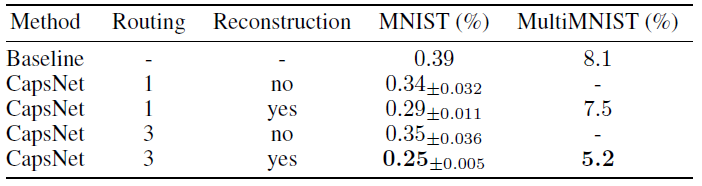
• The multi-layer capsule system achieves state-of-the-art performance on MNIST.
• Adding the reconstruction regularizer boosts the routing performance by enforcing the pose encoding in the capsule vector.
• CapsNet shows considerably better than a convolutional net at recognizing highly overlapping digits (MultiMNIST).

Individual Dimensions of a Capsule

• The above figure shows the reconstruction of perturbed version of the activity vector using decoder network.
• It shows that each dimension almost always represents width, stroke thickness, localized part and so on.

Conclusion

Pros

• Equivariance: CapsNet preserves position and pose information
• Requires less training data
• Promising for image segmentation and object detection
• Dynamic routing algorithm is good for overlapping objects
• Offers robustness to affine transformations
• Activation vectors are easier to interpret (rotation, thickness, skew…)

Cons

• Wondering if it work well on large images (e.g., ImageNet)
• Not state of the art on CIFAR-10
• Slow training and inference, due to the inner loop of routing algorithm
• A CapsNet cannot see two very close identical objects

References

• Paper: Dynamic Routing Between Capsules [Link]
• Blog: Hacker Noon [Link]
• Video: Capsule Networks by Aurélien Géron [Link]
• Video slide: Capsule Networks by Aurélien Géron [Link]