“Squeeze-and-Excitation Networks” suggests simple and powerful layer block to improve general convolutional neural network. It was presented in the conference on Computer Vision and Pattern Recognition (CVPR) 2018 by Jie Hu, Li Shen and Gang Sun.

Summary

  • Problem Statement
    • In general convolutional operation, the channel dependencies are implicitly embedded and these dependencies are entangled
  • Research Objective
    • To improve the representational power of a network by explicitly modelling the interdependencies between the channels of its convolutional features
  • Proposed Solution
    • Propose a architectural unit called “Squeeze-and-Excitation” (SE) block
    • Proposed mechanisim allows the network to perform feature recalibration, through which it can learn to use global information to selectively emphasise informative features and suppress less useful ones.
  • Contribution
    • SE blocks produce significant performance improvements for existing state-of-the-art deep architectures at minimal additional computational cost.
    • SENets won the first place on the ILSVRC 2017 classification submission.

Squeeze-and-Excitation Blocks

The Squeeze-and-Excitation block is a computational unit which can be constructed for any given transformation

\[F_{tr} : X \rightarrow U \\ X \in \mathbb{R}^{H^{'}\times W^{'} \times C^{'}} \\ U \in \mathbb{R}^{H\times W \times C}\]
  • Notation
    • \(F_{tr}\): convolutional operator
    • \(V=[v_1, v_2, \cdots, v_C]\): the learned set of filter kernels, where \(v_c\) refers to the parameters of the \(c\)-th filter
    • \(\star\): convolution
  • Outputs of \(F_{tr}\): \(U=[u_1, u_2, \cdots, u_C]\), where
\[u_c = v_c \star X = \sum_{s=1}^{C^{'}}{v^s_c \star x^s}\]

It represents a single channel of \(v_c\) which acts on the corresponding channel of \(X\).

In convolutional operation, since the output is produced by a summation through all channels, the channel dependencies are implicitly embedded, but these dependencies are entangled with the spatial correlation captured by the filters.

The goal is to ensure that the network is able to increase its sensitivity to informative features so that they can be exploited by subsequent transformations, and to suppress less useful ones.

This paper achieves this by two steps, squeeze and excitation.

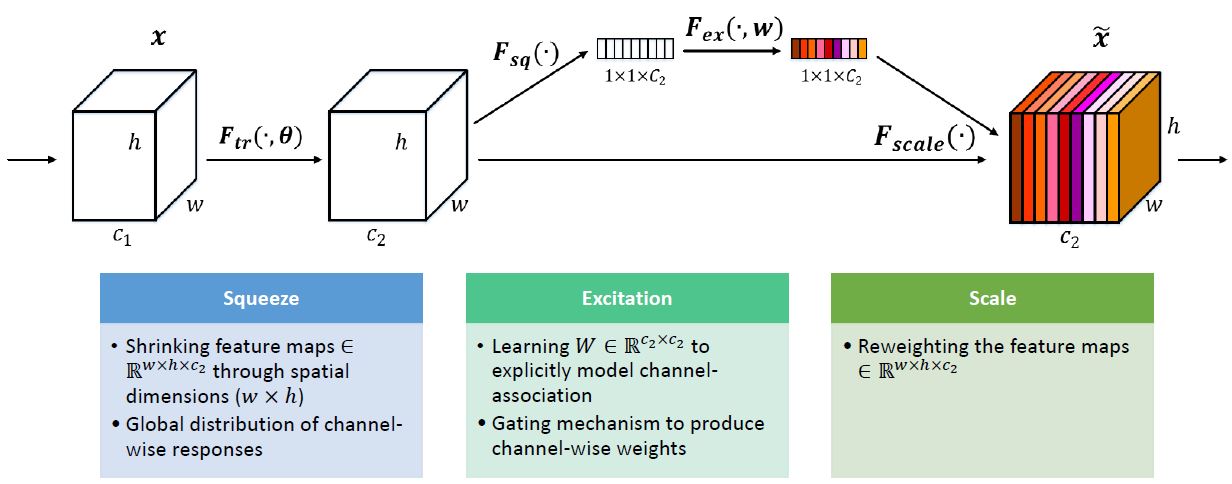SE block Figure 1: A Squeeze-and-Excitation block.

Squeeze: Global Information Embedding

Each of the learned filters operates with a local receptive field and consequently each unit of the transformation output is unable to exploit contextual information outside of this region. This is an issue that becomes more severe in the lower layers of the network whose receptive field sizes are small.

To handle this problem, this paper propose to squeeze global spatial information into a channel descriptor. This is achieved by using global average pooling to generate channel-wise statistics.

A statistic \(z \in \mathbb{R}^C\) is defined as,

\[z_c = F_{sq}(u_c)=\frac{1}{H\times W}\sum_{i=1}^{H} \sum_{j=1}^{W} u_c{(i,j)}\]

Excitation: Adaptive Recalibration

Excitation step aims to fully capture channel-wise dependencies. To fulfil this objective, the function must meet two criteria:

  1. it must be capable of learning a nonlinear interaction between channels
  2. it must learn a non-mutually-exclusive relationship since we would like to ensure that multiple channels are allowed to be emphasised.

To achieve this, this paper employ a simple gating mechanism with a sigmoid activation and ReLU function. And it formed a bottleneck by using two fully connected (FC) layers to limit model complexity and aid generalization.

\[s=F_{ex}(z,W)=\sigma(g(z,W))=\sigma(W_2 \delta(W_1z))\]
  • Notation
    • \(\sigma\): sigmoid function
    • \(\delta\): ReLU function
    • Parameters \(W_1 \in \mathbb{R}^{\frac{C}{r}}\times{C}\)
    • Parameters \(W_2 \in \mathbb{R}^{C}\times{\frac{C}{r}}\)
    • \(r\): reduction ratio

The final output of the block is obtained by rescaling the transformation output \(U\) with the activations which is channel-wise multiplication between the feature map \(u_c\) and the scalar \(s_c\).

\[\widetilde{x}_c=F{scale}(u_c,s_c)=s_c \cdot u_c\]

Exemplars: SE-Inception and SE-ResNet

SE block can be directly applied to transformations beyond standard convolutions.

  • For non-residual networks, such as Inception network, SE blocks are constructed for the network by taking the tranformation to be an entire Inception module.

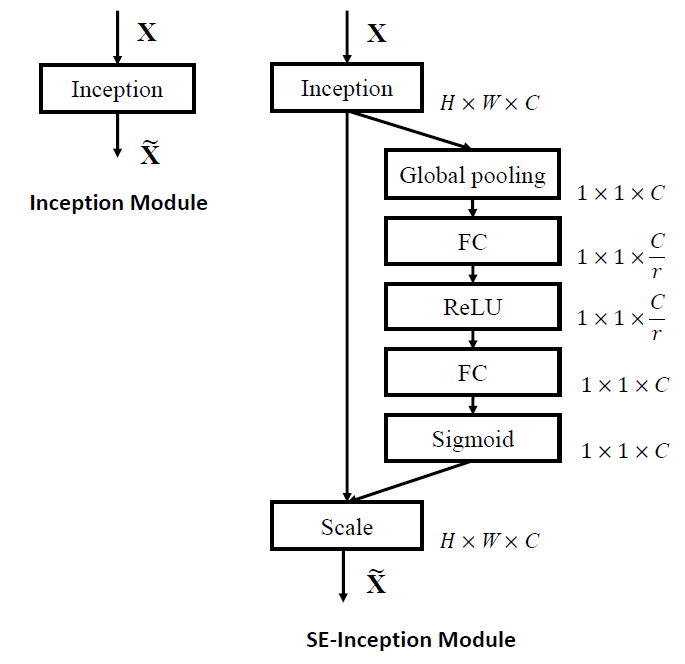SE-Inception Figure 2: The schema of the original Inception module (left) and the SE-Inception module (right).

  • For residual networks, the SE block transformation is taken to be the non-identity branch of a residual module.
    • Squeeze and excitation both act before summation with the identity branch.

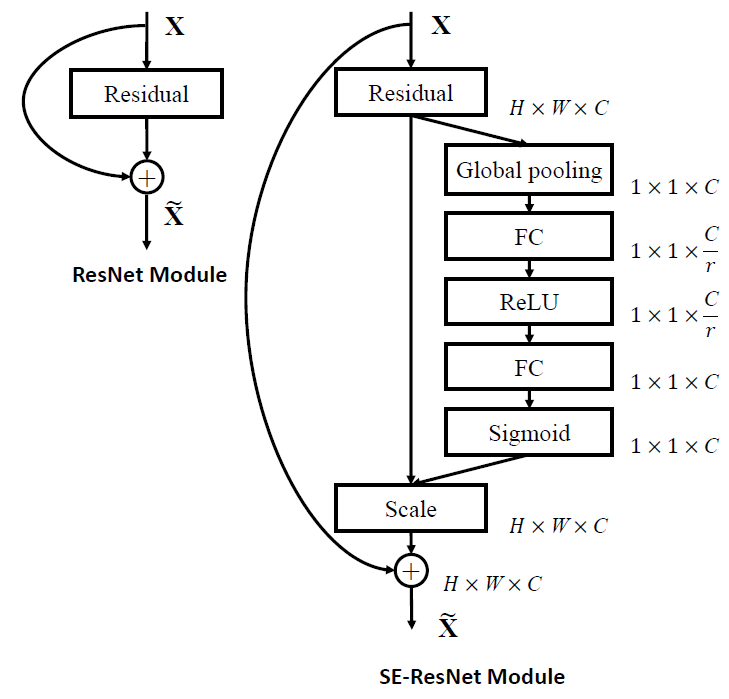SE-ResNet Figure 3: The schema of the original Residual module (left) and the SE-ResNet module (right).

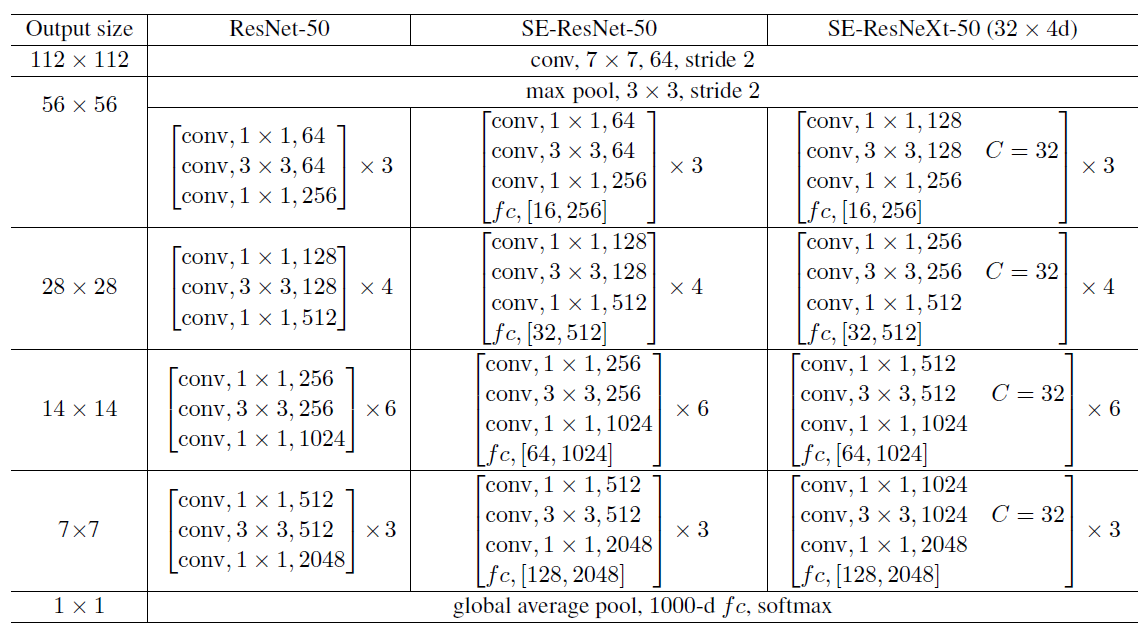Structure Figure 4: (Left) ResNet-50. (Middle) SE-ResNet-50. (Right) SE-ResNeXt-50 with a 32X4d template. The shapes and operations with specific parameter settings of a residual building block are listed inside the brackets and the number of stacked blocks in a stage is presented outside. The inner brackets following by fc indicates the output dimension of the two fully connected layers in an SE module.

Experimental Result

ImageNet Classification

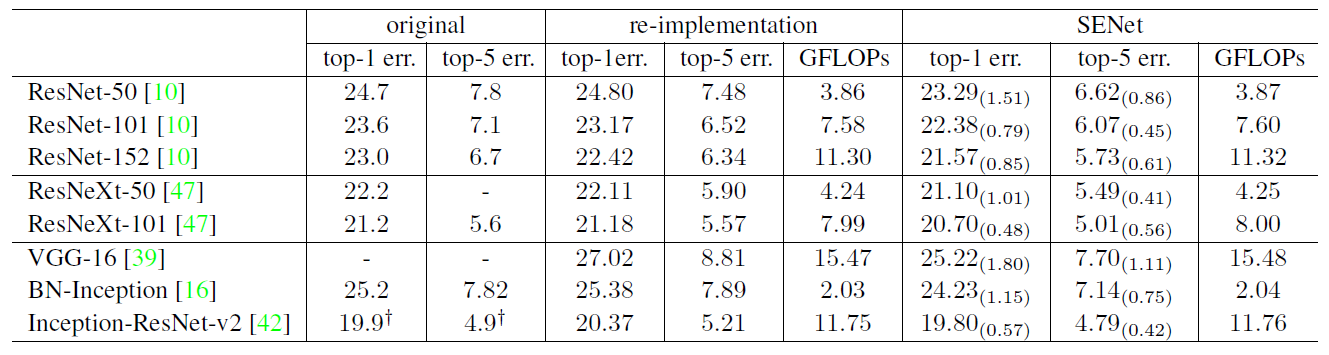Ex1 Figure 5: Single-crop error rates (%) on the ImageNet validation set and complexity comparisons. The original column refers to the results reported in the original papers. The SENet column refers to the corresponding architectures in which SE blocks have been added. The numbers in brackets denote the performance improvement over the re-implemented baselines. VGG-16 and SE-VGG-16 are trained with batch normalization.

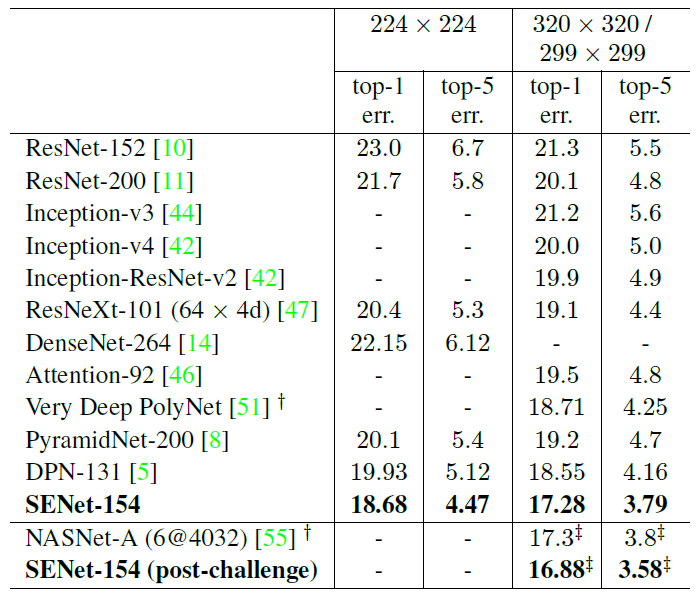Ex2 Figure 6: Single-crop error rates of state-of-the-art CNNs on ImageNet validation set. The size of test crop is 224 X 224 and 320 X 320 / 299 X 299. † denotes the model with a larger crop 331 X 331. ‡ denotes the post-challenge result. SENet-154 (post-challenge) is trained with a larger input size 320 X 320 compared to the original one with the input size 224 X 224.

Scene Classification

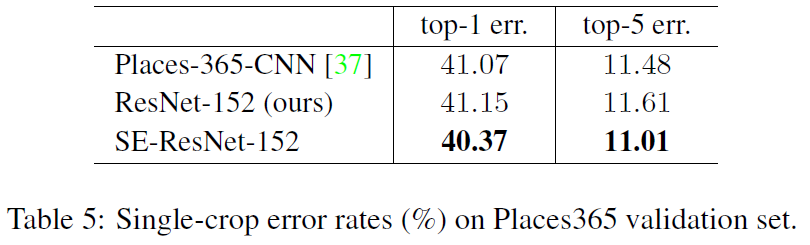Ex4 Figure 7: Single-crop error rates (%) on Places365 validation set.

Object Detection on COCO

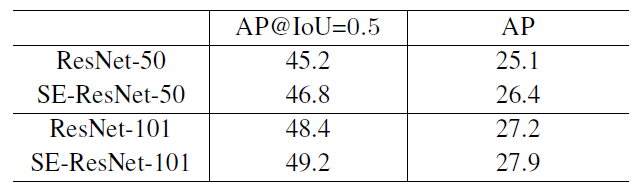Ex3 Figure 8: Object detection results on the COCO 40k validation set by using the basic Faster R-CNN.

Reduction Ratio

The reduction ratio \(r\) is an important hyperparameter which allows to vary the capacity and computational cost of the SE blocks in the model.

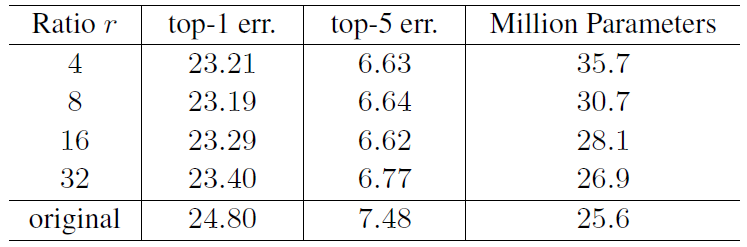Ex5 Figure 9: Single-crop error rates (%) on ImageNet validation set and parameter sizes for SE-ResNet-50 at different reduction ratios r. Here original refers to ResNet-50.

References

You May Also Enjoy