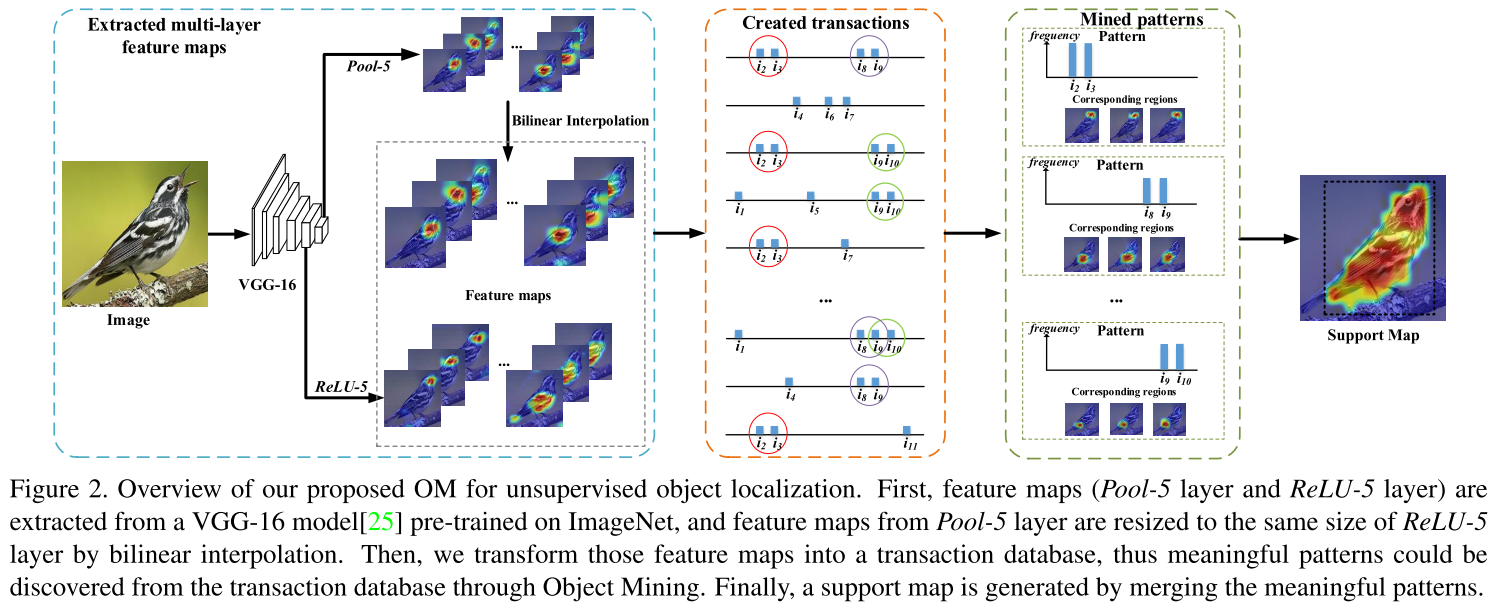
Sharing answer codes of mine about Programmers Level2. productMatrix.
Level 2: Matrix Multiplication
Problem Statement
The product \(C\) of two matrices \(A\) and \(B\) id defined as
where \(j\) is summed over for all possible values of \(i\) and \(k\). To multiply matrices, the number of columns in the left matrix and the number of rows in the right matrix must be the same. Given two matrices A and B that can be multiplied, complete the productMatrix function, which outputs the value of matrix multiplication.
Answer code without using Numpy (in Python 3)
# Answer code without using numpy
def productMatrix(A,B):
answer = [] # define return variable
# (i,j) * (j,k) = (i,k)
if range(len(A[0])) != range(len(B)): # Matrix product is impossible
return answer
for i in range(len(A)):
column=[]
for k in range(len(B[0])):
sum = 0
for j in range(len(A[0])):
sum += A[i][j]*B[j][k]
column.append(sum)
answer.append(column)
return answer
# Compile time: 23ms
Answer code using Numpy (in Python 3)
# Answer code using numpy
import numpy as np
def productMatrix(A,B):
# (i,j) * (j,k) = (i,k)
if range(len(A[0])) != range(len(B)): # Matrix product is impossible
return []
return (np.matrix(A)*np.matrix(B)).tolist()
# Compile time: 170ms
Clever answer code without using Numpy (in Python 3)
# Short answer code without using numpy
def productMatrix(A,B):
# (i,j) * (j,k) = (i,k)
if range(len(A[0])) != range(len(B)): # Matrix product is impossible
return []
return [[sum(a * b for a, b in zip(A_row, B_col)) for B_col in zip(*B)] for A_row in A]
# Compile time: 24ms