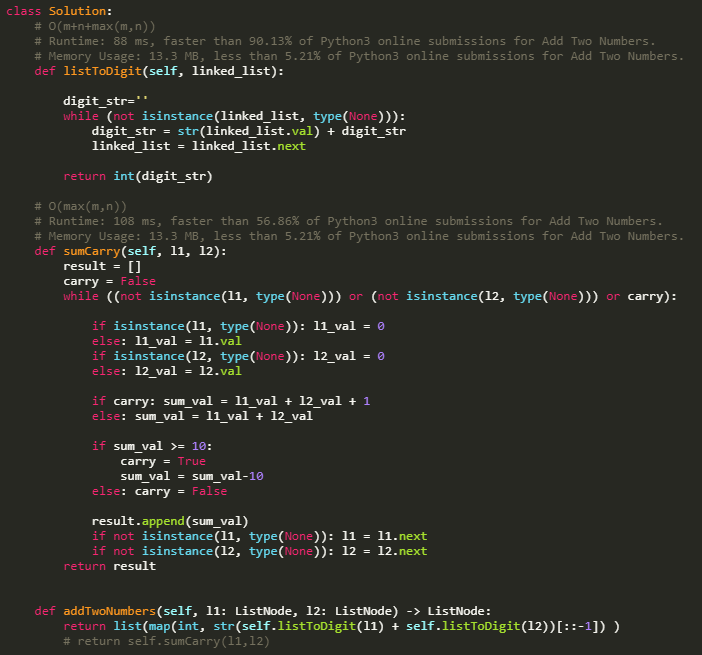
Sharing an answer code of mine about EquiLeader problem of Codility lesson 8.
Lesson 8: EquiLeader
A non-empty zero-indexed array A consisting of N integers is given.
The leader of this array is the value that occurs in more than half of the elements of A.
An equi leader is an index S such that 0 ≤ S < N − 1 and two sequences A[0], A[1], …, A[S] and A[S + 1], A[S + 2], …, A[N − 1] have leaders of the same value.
For example, given array A such that:
A[0] = 4
A[1] = 3
A[2] = 4
A[3] = 4
A[4] = 4
A[5] = 2
we can find two equi leaders:
0, because sequences: (4) and (3, 4, 4, 4, 2) have the same leader, whose value is 4. 2, because sequences: (4, 3, 4) and (4, 4, 2) have the same leader, whose value is 4. The goal is to count the number of equi leaders.
Write a function:
def solution(A)
that, given a non-empty zero-indexed array A consisting of N integers, returns the number of equi leaders.
For example, given:
A[0] = 4
A[1] = 3
A[2] = 4
A[3] = 4
A[4] = 4
A[5] = 2
the function should return 2, as explained above.
Assume that:
- N is an integer within the range [1..100,000];
- each element of array A is an integer within the range [−1,000,000,000..1,000,000,000].
Complexity:
- expected worst-case time complexity is O(N);
- expected worst-case space complexity is O(N), beyond input storage (not counting the storage required for input arguments).
Answer Code in Python 3
- Time complexity: \(O(N)\)
# Time complexity: O(n)
# you can write to stdout for debugging purposes, e.g.
# print("this is a debug message")
def solution(A):
# write your code in Python 3.6
candidate = None
candidate_length = 0
for i in range(len(A)):
if candidate_length == 0:
candidate_length += 1
candidate = A[i]
else:
if candidate != A[i]:
candidate_length -= 1
else:
candidate_length += 1
num_leader = A.count(candidate)
if num_leader <= len(A) // 2: return 0
else: leader = candidate
equi = 0
leader_now = 0
for i in range(0, len(A)-1):
if leader == A[i]:
leader_now += 1
if leader_now > (i+1) // 2 and num_leader - leader_now > (len(A)-(i+1)) // 2:
equi += 1
return equi