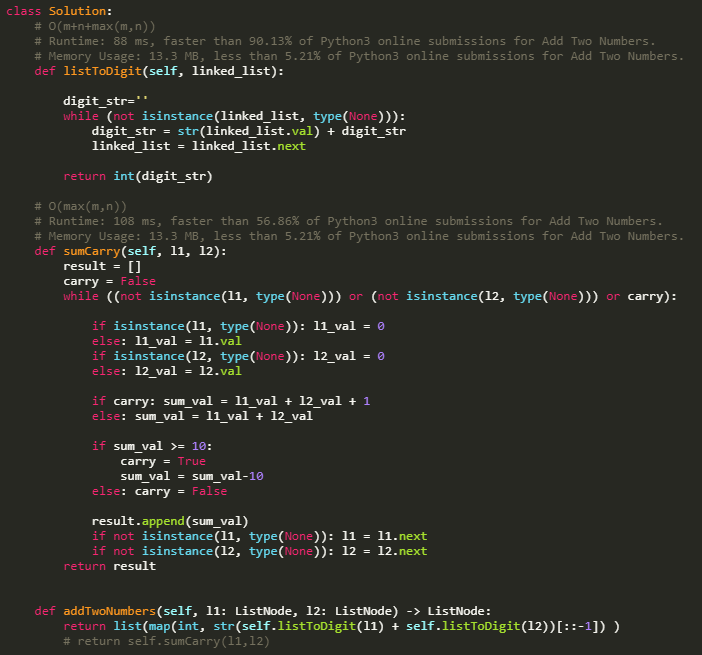
Sharing an answer code of mine about NumberSolitaire problem of Codility lesson 17.
Lesson 17: NumberSolitaire
A game for one player is played on a board consisting of N consecutive squares, numbered from 0 to N − 1. There is a number written on each square. A non-empty zero-indexed array A of N integers contains the numbers written on the squares. Moreover, some squares can be marked during the game.
At the beginning of the game, there is a pebble on square number 0 and this is the only square on the board which is marked. The goal of the game is to move the pebble to square number N − 1.
During each turn we throw a six-sided die, with numbers from 1 to 6 on its faces, and consider the number K, which shows on the upper face after the die comes to rest. Then we move the pebble standing on square number I to square number I + K, providing that square number I + K exists. If square number I + K does not exist, we throw the die again until we obtain a valid move. Finally, we mark square number I + K.
After the game finishes (when the pebble is standing on square number N − 1), we calculate the result. The result of the game is the sum of the numbers written on all marked squares.
For example, given the following array:
A[0] = 1
A[1] = -2
A[2] = 0
A[3] = 9
A[4] = -1
A[5] = -2
one possible game could be as follows:
- the pebble is on square number 0, which is marked;
- we throw 3; the pebble moves from square number 0 to square number 3; we mark square number 3;
- we throw 5; the pebble does not move, since there is no square number 8 on the board;
- we throw 2; the pebble moves to square number 5; we mark this square and the game ends.
The marked squares are 0, 3 and 5, so the result of the game is 1 + 9 + (−2) = 8. This is the maximal possible result that can be achieved on this board.
Write a function:
def solution(A)
that, given a non-empty zero-indexed array A of N integers, returns the maximal result that can be achieved on the board represented by array A.
For example, given the array
A[0] = 1
A[1] = -2
A[2] = 0
A[3] = 9
A[4] = -1
A[5] = -2
the function should return 8, as explained above.
Assume that:
- N is an integer within the range [2..100,000];
- each element of array A is an integer within the range [−10,000..10,000].
Complexity:
- expected worst-case time complexity is O(N);
- expected worst-case space complexity is O(N), beyond input storage (not counting the storage required for input arguments).
Answer Code in Python 3
- Time complexity: \(O(N)\)
- Space complexity: \(O(N)\)
# In Python 3.6
# Time complexity: O(N)
# Space complexity: O(N)
import math
def solution(A):
max_ = 0
n = len(A)
dp = [[-math.inf]*7 for _ in range(n)]
dp[0] = [-math.inf] + [A[0]]*6
for i in range(1, n):
for k in range(1, 7):
if i-k >= 0:
dp[i][k] = max(dp[i][k-1], max(dp[i-k])+A[i])
else:
dp[i][k] = dp[i][k-1]
return dp[n-1][6]