Learn about merge-sort, quick-sort, other sorting algorithms and their running time.
Sorting
Merge-Sort
- Merge-Sort uses divide-and-conquer algorithmic design pattern to sort a sequence S with n elements.
Divide-and-Conquer
- Divide: If the input size is smaller than a certain threshold, solve the problem directly using a straightforward method and return the solution. Otherwise, divide the input data into two or more disjoint subset.
- Conquer: Recursively solve the subproblems associated with the subsets.
- Combine: Take the solutions to the subproblems and merge them into a solution to the original problem.
Implementation
# In Python
# Merge two sorted Python lists S1 and S2 into properly sized list S
def merge(S1, S2, S):
i = j = 0
while i + j < len(S):
if j == len(S2) or (i<len(S1) and S1[i] < S2[j]):
S[i+j] = S[i] # copy ith element of S1 as next item of S
i += 1
else:
S[i+j] = S2[j] # copy jth element of S2 as next item of S
j += 1
# Sort the elements of Python list S using the merge-sort algorithm
def merge_sort(S):
n = len(S)
if n<2: return # list is already sorted
# Divide
mid = n // 2
S1 = S[0:mid] # copy of first half
S2 = S[mid:n] # copy of second half
# Conquer (with recursion)
merge_sort(S1) # sort copy of first half
merge_sort(S2) # sort copy of second half
# Merge results
merge(S1, S2, S) # merge sorted halves back into S
Running Time
- Algorithm merge-sort sorts a sequence S if size n in \(O(n\log n)\) time, assuming two elements of S can be compared in \(O(1)\) time.

Quick-Sort
Description of Quick-sort
- Quick-Sort algorithm uses divide-and-conquer technique to sort a sequence S using a simple recursive approach.
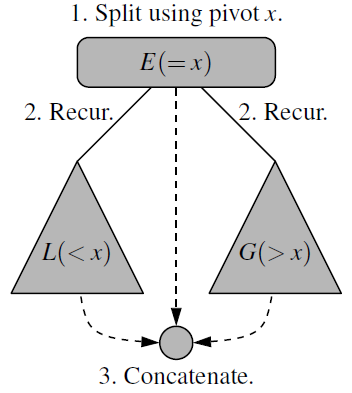
- Divide: If \(S\) has at least two elements, select a specific element \(x\) from S, which is called the pivot.
Remove all the elements from \(S\) and put them into three sequences:
- \(L\), storing the elements in \(S\) less than \(x\)
- \(E\), storing the elements in \(S\) equal to \(x\)
- \(G\), storing the elements in \(S\) greater than \(x\)
- Conquer: Recursively sort sequences \(L\) and \(G\).
- Combine: put back the elements into \(S\) in order by first inserting the elements of \(L\), then those of \(E\), and finally those of \(G\).
Implementation
# In Python
# Sort the elements of queue S using the quick-sort algorithm
def quick_sort(S):
n = len(S)
if n<2: return # list is already sorted
# Divide
p = S.first() # using first as arbitrary pivot
L = LinkedQueue()
E = LinkedQueue()
G = LinkedQueue()
while not S.is_empty(): # divide S into L, E, and G
if S.first() < p
L.enqueue(S.dequeue())
elif p < S.first():
G.enqueue(S.dequeue())
else:
E.enqueue(S.dequeue())
# Conquere (with recursion)
quick_sort(L) # sort elements less than p
quick_sort(G) # sort elements greater than p
# Concatenate results
while not L.is_empty():
S.enqueue(L,dequeue())
while not E.is_empty():
S.enqueue(E.dequeue())
while not G.is_empty():
S.enqueue(G.dequeue())
Running Time
- Quick-Sort runs in \(O(n\log n)\) time, and \(O(n^2)\) in the worst-case.
- Randomized Quick-Sort gives \(O(n\log n)\) expected running time.
- Memory: \(O(\log n)\)
Bubble Sort
- In bubble sort, we start at the beginning of the array and swap the first two elements if the first is greater than the second
- Then, we go to the next pair, and so on, continuously making sweeps of the array until it is sorted.
- Runtime: \(O(n^2)\) average and worst case, Memory: \(O(1)\).
Selection Sort
- Selection sort is simple but inefficient.
- Find the smallest element using a linear scan and move it to the front (swapping it with the front element).
- Continue doing this until all the elements are in place
Insertion Sort
- Insertion sort is relatively efficient for small lists and mostly sorted list.
- It works by taking elements from the list one by one and inserting them in their correct position into a new sorted list.
- Runtime: \(O(n^2)\), Memory: \(O(1)\)
Heap Sort
- Heap sort works by determining the largest (or smallest) element of the list, placing that at the end (or beginning) of the list.
- Then, continuing with the rest of the list by using a data structure heap (a special type of binary tree).
- Runtime: \(O(n\log(n))\), Memory: \(O(1)\)
Radix Sort
- Radix sort is a sorting algorithm for integers that takes advantage of the fact that integers have a finite number of bits.
- We iterate through each digit of the number, grouping numbers by each digit.
- Then, we sort each of these groupings by the next digit.
- Runtime: \(O(kn)\) (\(n\) is the number of elements and \(k\) is the number of passes of the sorting algorithm)
Comparison and Non-comparison Sort
Comparison Sort
- Comparison sort is a type of sorting algorithm that only reads the list elements through a single comparison operation and
determines which of two elements should occur first in the final sorted list.
- Comparison: \(a_i < a_j, a_i \leq a_j, ...\)
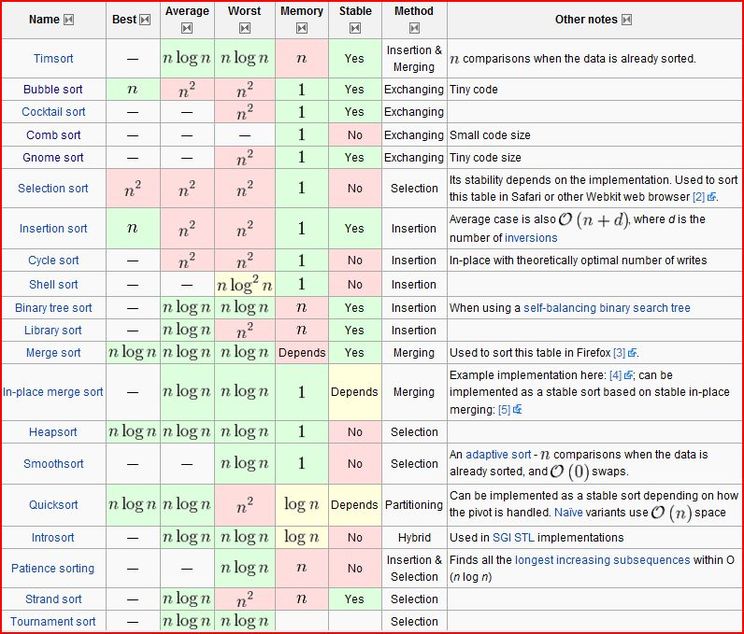
- Examples : Bubble sort, Insertion sort, Selection sort, Quick sort, Heap sort, Merge sort, Odd-even sort, Cocktail sort, Cycle sort, Merge insertion sort, Smoothsort, Timsort
- Limitations of Comparison Sorting
- To sort \(n\) elements, comparison sorts must make \(\Omega(n\log n)\) comparisons in the worst case.
- That is a comparison sort must have lower bound of \(\Omega(n\log n)\) comparison operations, which is known as linear or linearithmic time.
Non-comparison Sort
- Non-comparison sort perform sorting without comparing the elements rather by making certain assumptions about the data.
- Examples:
- Counting sort (indexes using key values)
- Radix sort( examines individual bits of keys)
- Bucket sort( examines bits of keys)
- These are linear sorting algorithms.
- They make certain assumptions about the data.
- Examples:
Sorting Algorithm Comparison