Learn about Binary Search which is a simple and very useful algorithm whereby many linear algorithms can be optimized to run in logarithmic time.
Binary Search
Binary Search is a search algorithm that finds the position of a target value within a sorted array. It compares the target value to the middle element of the array, if they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half until it is successful. If the search ends with the remaining half being empty, the target is not in the array.
- Class: Search algorithm
- Data structure: Array
- Worst-case performance: \(O(\log N)\)
- Best-case performance: \(O(1)\)
- Average performance: \(O(\log N)\)
- Worst-case space complexity: \(O(1)\)
Process
We ignore half of the elements just after one comparison.
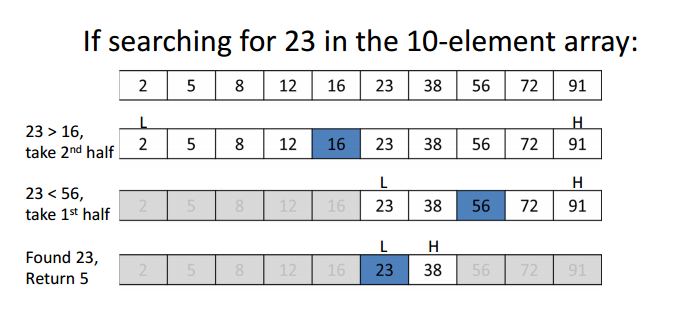
- Compare \(x\) with the middle element.
- If \(x\) matches with middle element, we return the mid index.
- Else if \(x\) is greater than the mid element, then \(x\) can only lie in right half subarray after the mid element. So we recur for right half.
- Else if \(x\) is smaller, recur for the left half.
Implementation
- Recursive implementation
# Python Program for recursive binary search.
# Returns index of x in arr if present, else -1
def binarySearch (arr, l, r, x):
# Check base case
if r >= l:
mid = l + (r - l)/2
# If element is present at the middle itself
if arr[mid] == x:
return mid
# If element is smaller than mid, then it
# can only be present in left subarray
elif arr[mid] > x:
return binarySearch(arr, l, mid-1, x)
# Else the element can only be present
# in right subarray
else:
return binarySearch(arr, mid+1, r, x)
else:
# Element is not present in the array
return -1
# Test array
arr = [ 2, 3, 4, 10, 40 ]
x = 10
# Function call
result = binarySearch(arr, 0, len(arr)-1, x)
if result != -1:
print "Element is present at index %d" % result
else:
print "Element is not present in array"
- Iterative implementation
# Python code to implement iterative Binary Search.
# It returns location of x in given array arr if present, else returns -1
def binarySearch(arr, l, r, x):
while l <= r:
mid = l + (r - l)/2;
# Check if x is present at mid
if arr[mid] == x:
return mid
# If x is greater, ignore left half
elif arr[mid] < x:
l = mid + 1
# If x is smaller, ignore right half
else:
r = mid - 1
# If we reach here, then the element
# was not present
return -1
# Test array
arr = [ 2, 3, 4, 10, 40 ]
x = 10
# Function call
result = binarySearch(arr, 0, len(arr)-1, x)
if result != -1:
print "Element is present at index %d" % result
else:
print "Element is not present in array"
Covering Holes Example
Problem Statement
You are given \(n\) binary values \(x_0, x_1, ... , x_{n−1}\), such that \(x_i \in {0, 1}\). This array represents holes in a roof (1 is a hole). You are also given \(k\) boards of the same size. The goal is to choose the optimal (minimal) size of the boards that allows all the holes to be covered by boards.
Solution
The size of the boards can be found with a binary search. If size \(x\) is sufficient to cover all the holes, then we know that sizes \(x+1, x+2, ... , n\) are also sufficient. On the other hand, if we know that \(x\) is not sufficient to cover all the holes, then sizes \(x−1, x−2, ... , 1\) are also insufficient.
def boards(A, k):
n = len(A)
beg = 1
end = n
result = -1
while beg <= end:
mid = (beg+end) / 2
if check(A, mid) <= k:
end = mid - 1
result = mid
else:
beg = mid + 1
return result
To check whether size \(x\) is sufficient, we can go through all the indices from the left to the right and greedily count the boards. We add a new board only if there is a hole that is not covered by the last board.
def check(A, s):
n = len(A)
boards = 0
last = -1
for i in range(n):
if A[i] == 1 and last < i:
boards += 1
last = i+s-1
return boards



