Learn about graph, graph representations, graph traversals and their running time.
Graph
- Graph is a collection of nodes with edges between (some of) them.
- Tree is a type of graph, a tree is a connected graph without cycles.
- Graphs can be either directed or undirected.
- The graph might consist of multiple isolated subgraphs. If there is a path between every pair of vertices, it is called a connected graph.
- The graph can also have cycles or not. An acyclic graph is one without cycles.
Graph Representations
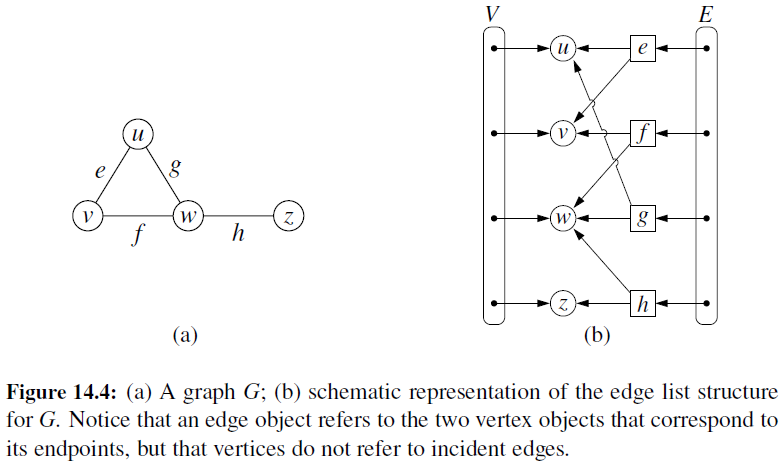
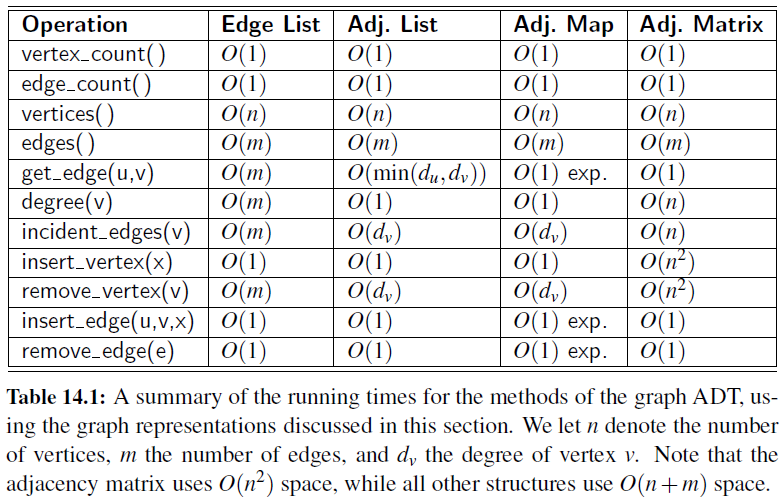
Edge List
- Maintain an unordered list of all edges
- But there is no efficient way to locate a particular edge (u,v), or the set of all edges incident to a vertex v.
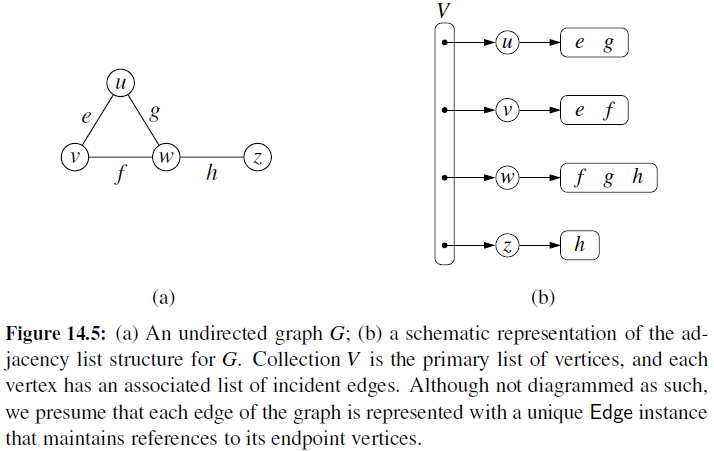
Adjacency List
- Every vertex (or node) stores a list of adjacent vertices.
- In an undirected graph, an edge like (a,b) would be stored twice.
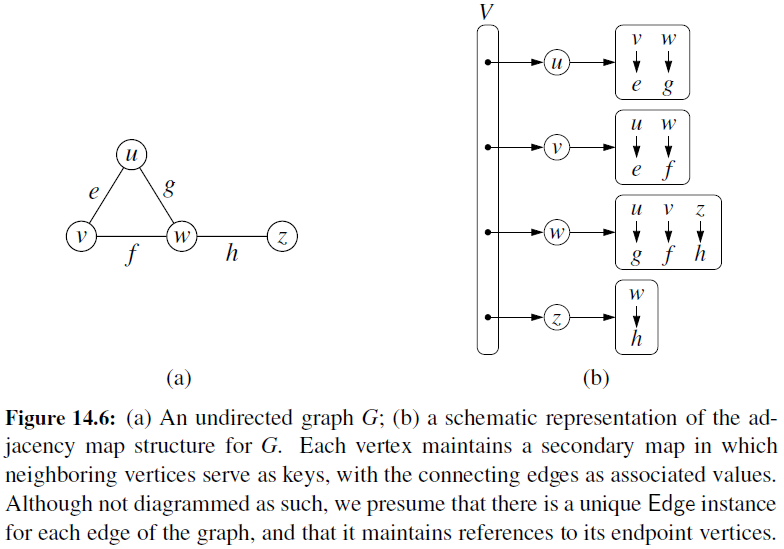
Adjacency Map
- It is very similar to an adjacency list, but the secondary container of all edges incident to a vertex is organized as a map, rather than as a list, with the adjacent vertex serving as a key.
- This allows for access to a specific edge (u,v) in \(O(1)\) expected time.
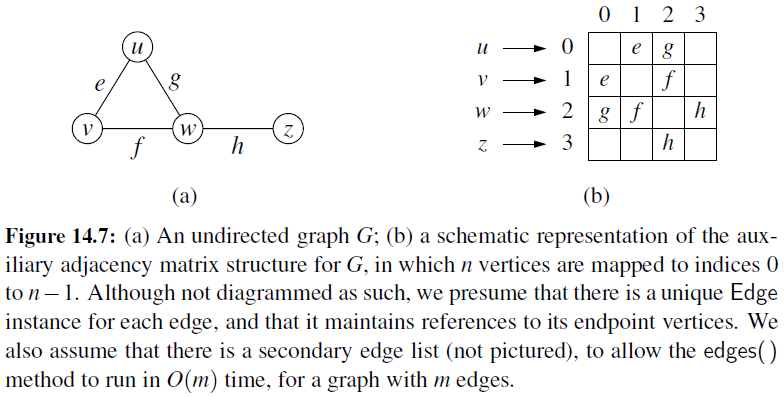
Adjacency Matrix
- It provides worst-case \(O(1)\) access to a specific edge (u,v) by maintaining an \(n \times n\) matrix, for a graph with \(n\) vertices.
- Each entry is dedicated to storing a reference to the edge (u,v) for a particular pair of vertices u and v.
Time Complexity
Graph Traversals
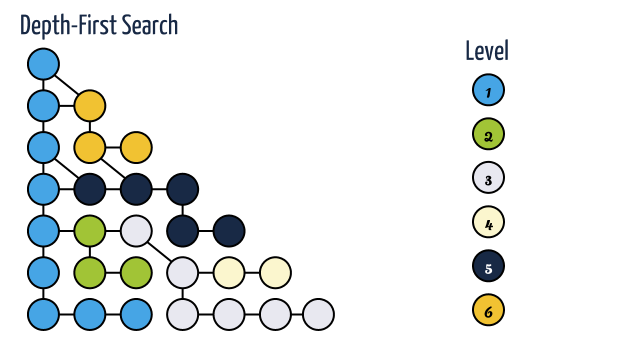
Depth-First Search
- Depth-first search is useful testing a number of properties of graphs, including whether there is a path, and whether or not a graph is connected.
- Implementation
# Perform DFS of the undiscovered portion of Graph g starting at Vertex u.
# discovered is a dictionary mapping each vertex to the edge that was used to discover it during the DFS.
# Newly discovered vertices will be added to the dictionary as a result.
def DFS(g, u, discovered):
for e in g.incident_edges(u): # for every outgoing edge from u
v = e.opposite(u) # the other vertex connected by u
if v not in discovered: # v is an unvisited vertex
discovered[v] = e # e is the tree edge that discovered v
DFS(g, v, discovered) # recursively explore from v
- Time complexity
- Let G be an undirected graph with n vertices and m edges. A DFS traversal of G can be performed in \(O(n+m)\) time.
- Let G be a directed graph with n vertices and m edges. A DFS traversal of G can be performed in \(O(n+m)\) time.
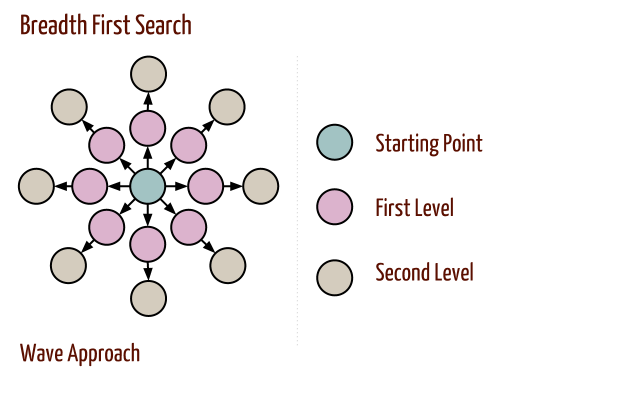
Breadth-First Search
- Breadth-first search proceeds in rounds and subdivides the vertices into levels.
- Implementation
# Perform BFS of the undiscovered portion of Graph g starting at Vertex s.
# discovered is a dictionary mapping each vertex to the edge that was used to discover it during the BFS.
# Newly discovered vertices will be added to the dictionary as a result.
def BFS(g, s, discovered):
level = [s] # first level includes only s
while len(level) > 0:
next_level = [] # prepare to gather newly found vertices
for u in level:
for e in g.incident_edges(u): # for every outgoing edge from u
v = e.opposite(u)
if v not in discovered: # v is an unvisited vertex
discovered[v] = e # e is the tree edge that discovered v
next_level.append(v) # v will be further considered in next pass
level = next_level # relabel 'next' level to become current
- Time complexity
- Let G be a graph with n vertices and m edges represented with the adjacency list structure. A BFS traversal of G takes \(O(n+m)\) time.
Bidirectional Search
- Bidirectional search is used to find the shortest path between a source and destination node.
- It operates by essentially running two simultaneous breadth-first searches, one from each node.
- When their searches collide, we have found a path.
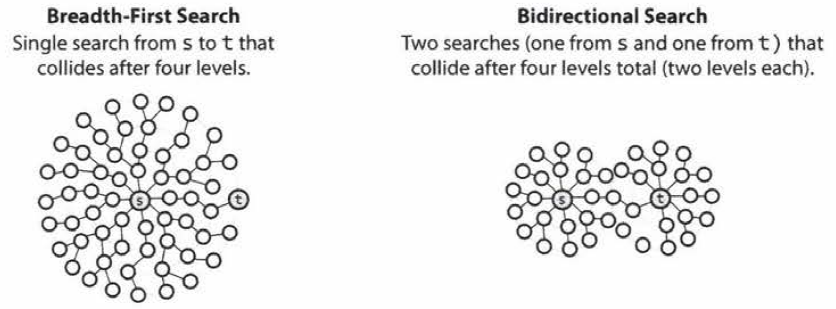
- To see why this is faster, consider a graph where every node has at most \(k\) adjacent nodes and the shortest path from node \(s\) to node \(t\) has length \(d\).
- In breadth-first search, it takes \(O(k^d)\) times since it search up to \(k\) nodes in one level and do this \(d\) times.
- In bidirectional search, it takes \(O(k^{d/2})\) times since two searches would collide after approximately \(d/2\) levels.
Minimum Spanning Tree
Problem Definition
- Given an undirected, weighted graph G, we are interested in finding a tree T that contains all the vertices in G and minimizes the sum
- Spanning tree: a tree that contains every vertex of a connected graph G.
-
Minimum Spanning Tree (MST) problem is to compute a spanning tree T with smallest total weight.
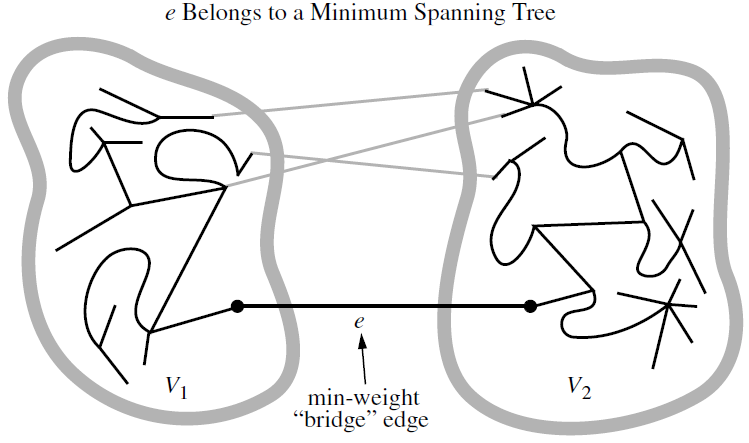
- Proposition
Let \(G\) be a weighted connected graph, and let \(V_1\) and \(V_2\) be a partition of the vertices of \(G\) into two disjoint nonempty set. Furthermore, let \(e\) be an edge in \(G\) with minimum weight from among those with one endpoint in \(V_1\) and the other in \(V_2\). There is a minimum spanning tree \(T\) that has \(e\) as one of its edges.
Kruskal’s Algorithm
- Kruskal’s Algorithm maintains a forest of clusters, repeatedly merging pairs of clusters until a single cluster spans the graph which is greedy method.
# Compute a MST of a graph using Kruskal's algorithm
# Return a list of edges that comprise the MST.
# The elements of the graph's edges are assumed to be eights.
def MST_Kruskal(g):
tree = [] # list of edges in spanning tree
pq = HeapPriorityQueue() # entries are edges in G, with weights as key
forest = Partition() # keeps track of forest clusters
position = {} # map each node to its Partition entry
for v in g.vertices():
position[v] = forest.make_group(v)
for e in g.edges():
pq.add(e.element(), e) # edge's element is assumed to be its weight
size = g.vertex_count()
while len(tree) != size-1 and not pq.is_empty():
# tree not spanning and unprocessed edges remain
weight, edge = pq.remove_min()
u, v = edge.endpoints()
a = forest.find(position[u])
b = forest.find(position[v])
if a!=b:
tree.append(edge)
forest.union(a,b)
return tree



